QUANTUM ENTANGLEMENT AND THE STRUCTURE OF SPACE-TIME

The physics of the Universe, at a fundamental scale, is so different from our macroscopic world that it seems like science fiction. In this article, we will explore an incredible and strange relationship between quantum entanglement, exotic objects called "wormholes," and the connectivity of space-time itself. Quantum entanglement acts as the "glue" that maintains the structure of space-time itself, so that if entanglement is reduced, space-time disperses, thus losing its fundamental structure.

Black holes and Einstein-Rosen bridges

The Schwarzschild solution to the equations of general relativity includes an eternal black hole with spherical symmetry whose metric is:

This metric presents a singularity on the horizon for r=2GM, however, if we make the following change of coordinates:

The singularity at the horizon disappears, which implies that (classically) this singularity is not physically real since it does not persist through any change in the reference frame. These coordinates are called Kruskal coordinates, and if we draw the graph with the values au and v, we obtain four disconnected zones separated by an event horizon:

Zones I and II represent the exterior of the black hole while zones III and IV represent the interior of the black hole and have an asymptotically AdS geometry (this is basically the shape of a hyperboloid see for example this article ).

Since these zones are causally disconnected, the four zones can be interpreted as a system of two black holes (each with its interior and exterior) with AdS geometry. that do not interact with each other. The central region of the diagram is a region common to both black hole systems and is called the "Einstein-Rosen bridge." This "bridge" is the region where the throats of the two AdS geometries meet:

Since this area represents the union of two different space-times (which could be in the same Universe or in different Universes if we admit the existence of a Multiverse) and is shaped like a tube, it is also called a wormhole.

Subsequent work showed that this "bridge" is not traversable because it closes before any signal can cross it. This is why we say that the two black holes are causally disconnected.

The AdS/CFT duality

The most cited theoretical physics paper in history is Juan Maldacena's "The large N limit of superconformal field theories and supergravity" . This paper establishes a surprising equivalence: An AdS spacetime formulated in d dimensions is equivalent to a (conformal) quantum system formulated on the AdS edge (in d-1 dimensions). The amazing thing about this equivalence is that both systems appear completely different: the first system (AdS geometry) is a system with constant gravity and negative curvature, while the second system (CFT) is a gravity-free quantum field system formulated in a spacetime with one less dimension. Despite these differences, both systems have the same set of symmetries and are therefore described by the same physics.

In the case of the two black hole system above, the AdS/CFT duality tells us that the geometry of both holes is described by two CFT systems living on the asymptotic edge of the AdS geometry.

Quantum entanglement and the connectivity of space-time

A CFT system can be described by a wave function, in the case of two CFTs without any interaction the total Hilbert space will simply be the product of both systems:

By the AdS/CFT duality this state corresponds to two completely independent space-times.

The question we ask now is: What happens if we consider two entangled states? An entangled state of two copies of a CFT would be described as follows:

This entangled state is the sum of the product of the states Ei of the two CFTs (the exponential factor represents the "degree of entanglement" as in the Bloch sphere), which is therefore the product of the Hilbert spaces H1*H2. But as we have just seen, the product H1*H2 is interpreted on the gravitational side as the states of a spacetime with two completely disconnected components. Therefore, the previous entangled state must be considered as a superposition of two disconnected spacetimes , that is, our system of two black holes with AdS geometry joined by a non-traversable Einstein-Rosen bridge.

Put schematically:

Where B is the inverse of the temperature of the quantum system and Ei are the states of the two CFTs.

This means that entangling the states of both CFTs is equivalent to creating an Einstein-Rosen bridge between the dual space-times.

The interpretation of this is truly surprising: the connectivity between the states of a classical space-time arises from the entanglement between the degrees of freedom of two quantum systems.

Building and destroying space-time with entanglement

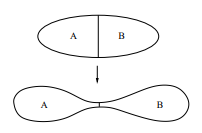
In a famous paper entitled " Holographic derivation of entanglement entropy from AdS/CFT ," physicists Ryu and Takayanagi showed that the total amount of entanglement entropy between two complementary systems A and B is proportional to the minimum surface area coinciding with the boundary of one of the systems. To see this more clearly, consider a sphere divided into two hemispheres, A and B:

The surface Á is the minimal Ryu-Takayanagi surface and separates the systems A and B. The Ryu-Takayanagi formula then implies that the entanglement entropy between A and B is proportional to the surface of Á, namely:

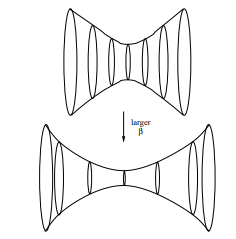
Next we will do an impressive experiment: we will vary the amount of entanglement between areas A and B and analyze what happens to the spacetime contained between A and B. To decrease the entanglement entropy between A and B we simply decrease the temperature of the dual CFT (remember that the exponent B in the CFT wavefunction expression is the inverse of the temperature). By the Ryu-Takayanagi formula, decreasing S(A) will decrease the area of Á. Taking into account the AdS/CFT duality, the area Á is the surface that separates the two disconnected AdS spacetimes, that is, the Einstein-Rosen bridge, therefore, decreasing the entanglement between A and B is equivalent to separating or disconnecting classical spacetime. This can be interpreted as a destruction of the connectivity of spacetime itself.

By decreasing the entanglement between A and B, the surface area between these two zones decreases (left), which is equivalent to "puncturing" or separating the two space-times with negative curvature in the AdS part of the duality (right).

In fact, given two points C and D located on the edges A and B of the sphere, we can calculate the distance between them using an expression called the correlation function.

This calculation shows that as the mutual information between C and D decreases, that is, as entanglement decreases, the correlation function between C and D tends to zero, which means that the shortest distance between them tends to infinity. In the dual picture, this implies that the two AdS spacetimes separate until they become independent, which is equivalent to the disappearance of the connectivity of the dual classical spacetime.

All of this seems to indicate a profound relationship between quantum entanglement, wormholes, and the "seams" of classical space-time. In fact, there is a conjecture called ER=EPR in which physicists Juan Maldacena and Leonard Suskind speculate on the possibility that all entangled particles are connected by a kind of quantum wormhole. On the other hand, although the Einstein-Rosen bridge of the Schwarzschild black hole is non-traversable, ways have been found to make the wormhole traversable. This can be achieved, for example, by entangling the states of two magnetic black holes.

Little by little, physicists are unraveling the deepest secrets of space-time. Will we be able to discover the most fundamental laws of space-time?

Sources:

Building up spacetime with quantum entanglement