OUR STRANGE FOUR-DIMENSIONAL UNIVERSE

When we look around us, we see a three-dimensional world: objects are made up of the three usual spatial dimensions. Although we all know that these objects move in time, we tend to assign to time a reality independent of three-dimensional objects. However, once again, reality seems to surpass fiction: our real Universe has four dimensions, and as we will see in this article, these dimensions are closely connected. In this article, we will visualize our four-dimensional Universe and see its measurable effects. As if we lived in Plato's cave, we only see the three-dimensional shadows of objects moving in a four-dimensional Universe, which leads us to interpret these "shadows" as strange and "exotic" phenomena.

Welcome to our strange four-dimensional world!

Visualizing the fourth dimension

Let's consider an everyday object like a 4-meter ladder. This ladder is at rest relative to an observer named Fernando and has two clocks synchronized at both ends. At a given moment, Fernando stands right in the middle of the ladder and measures the distance between both ends at the same instant in time (for Fernando, the clocks at both ends show the same time). The measured length is, of course, 4 meters . Next, we'll begin to see the "shadows" of objects moving in four dimensions: consider the scene above seen from an observer named Maria, who passes right over the ladder in a rocket traveling at 60% of the speed of light. From Maria's reference frame, the ship is at rest, and it is the ladder that is approaching 60% of the speed of light. When the ladder reaches the ship and Maria observes Fernando taking the measurement, she notices something "surprising": from her reference frame , Fernando doesn't measure both ends at the same time! He first measures the front end, then the back end. On the other hand, the ship's measurement sensor, which is activated just when the forward end of the ladder is at the height of the ship's nose and is deactivated just when the rear end of the ladder has passed said sensor, shows a measurement of 3.2 meters! (1). Later, when they both meet at the cafeteria, Fernando tells Maria that the ladder measures 4 meters, but she insists that the real measurement is 3.2 meters. Furthermore, Maria tells Fernando that he did not measure it at the same time, while Fernando insists that she is the one who did not measure it at the same instant. What the hell is going on here? Who is right? To try to understand what is happening, let's draw the space-time diagram of the previous scene.

A reference system S´ that moves at a speed V with respect to a system at rest S would be represented as follows:

The vertical axis represents time, and the horizontal axis represents space. System S at rest only moves in time and covers an interval T, while system S' in that interval T has also moved in space a distance vT. In this way, we observe a fundamental characteristic of space-time diagrams: the moving system has axes inclined with respect to the system at rest:

The x´ axis represents the instant t´=0 in the moving reference system. The successive instants of time t´=1, t´=2 etc. are represented by lines parallel to the x´ axis.

x´ axis. Similarly, the distances x´=1, x´=2 etc. are represented by lines parallel to the t´ axis. In the reference frame at rest S, the spatial and temporal lines are represented in the usual way parallel to the x and t axes.

Since the axes are inclined in the reference system S´, the lines of simultaneity of both systems are different, that is, events that are simultaneous in S are not simultaneous in S ´and vice versa:

Events A and B occur at the same instant in the reference system at rest S (instant t=4) but in the reference system in motion S´, event B occurs first (instant t´=2) and then event A (instant t´=3.5) (Image taken from: TikZ.net )

Events A and B occur simultaneously in reference frame S' (time t' = 3) but are not simultaneous in S (first A occurs at t = 3.2 and then B at t = 5.2). (Image taken from: TikZ.net )

Now we are ready to visualize the fourth dimension by superimposing both reference systems:

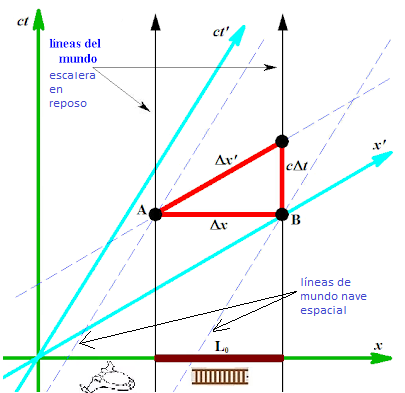
The vertical black lines represent the motion of the ends of the ladder at rest, with length Lo. The dashed inclined lines represent the ends of the moving spacecraft. Events A and B are the points in spacetime where the ends of the ladder coincide with the ends of the spacecraft (this can be seen in the figure where the two "worldlines" intersect).

The key point is the following: for Fernando the lines of simultaneity are horizontal and therefore the length measured at the same instant is delta-x

(length Lo), however, for Maria the lines of simultaneity are inclined and therefore the measurement made at a certain instant in time is the length delta-x´

If we graduate the two axes we can appreciate the magnitudes measured by both observers:

(Image taken from: TikZ.net )

As we can see in the diagram, the length Lo in S is 4 meters while the length L in S' is only 3.2m (2). Furthermore, while for Fernando events A and B are simultaneous, for Maria they are not; for her, simultaneous events are events A and B´. However, for Fernando, the interval AB´ not only has units of length but also has units of time— that is, it has a mixture of spatial and temporal magnitudes. We have just visualized the fourth dimension of a three-dimensional object moving in a four-dimensional world!

Now we're in a position to understand what's really going on: the worldlines we drew in the diagrams above are drawn in a four-dimensional space-time, and different observers measure different three-dimensional "slices" of the same four-dimensional object. These slices have different values of space and time: what is space for one observer is time for another, and vice versa. Reality has four dimensions, but we, as three-dimensional beings, can only detect three-dimensional shadows! Isn't this truly incredible?

In the figure on the left, Fernando, at rest in front of the ladder, measures "horizontal slices" of the ladder. For him, events A and B corresponding to the ends of the ladder are simultaneous, and therefore he detects a length Lo = 4 m. In the figure on the right, Maria experiences a Lorentz factor of 1.25 since she is traveling at 60% of the speed of light with respect to the ladder. Maria measures inclined "slices" of the ladder, and events A and B are not simultaneous: she first measures end A and then end B. For Fernando, Maria is measuring a mixture of spatial and temporal intervals!

The leap from Special Relativity to General Relativity

Imagine the following thought experiment: a person is riding an accelerating carousel. Outside the carousel, at rest, two metal spheres are placed 10 meters apart. Each time the carousel completes a full revolution, the observer opens their eyes and observes the spheres. On the first revolution, the carousel has barely accelerated, and therefore the observer sees the two spheres 10 meters apart. On the second revolution, the carousel is already traveling at 0.5 cy, so the observer will detect that the spheres are closer due to relativistic length contraction. On the third revolution, the speed is already 0.8 cy, so the spheres will appear even closer. With the fourth revolution, at 0.9 c, the process of the spheres "coming closer" continues:

(Image taken from: The Theory of Relativity )

If the carousel's acceleration is not constant but variable, then the observer will see the two masses accelerating toward each other. This effect implies that objects measured in an accelerated reference frame will be detected as attracting each other because the distance between them is shortening due to relativistic effects. Einstein realized that an observer inside a metal box accelerating in space would not be able to distinguish from within whether the box is accelerating or immersed in a gravitational field. This idea constitutes one of the fundamental pillars of general relativity: there is no force of attraction between massive objects; it is the space between them that is being compressed:

The vision we have just given is only intuitive since it is not only space that is compressed but time also dilates:

Therefore, this process occurs not only in 3D space but also in four-dimensional space-time. In general relativity, the existence of four-dimensional space-time becomes even more evident than in special relativity: gravity is now (locally) equivalent to an accelerated reference frame, and bodies follow trajectories (geodesics) in a curved 4-dimensional space-time. The Earth follows a geodesic through the curved 4D space-time produced by the Sun's gravity.

It is not difficult to imagine the astonishment and perplexity of the scientific community and subsequently the entire world when Einstein published his theory in 1915. The theory of relativity has been verified by a multitude of experiments since then and constitutes one of the most important advances in human knowledge.

Grades

(1) For a reference system moving at 60% of the speed of light the Lorentz factor is 1.25 therefore the relativistic contraction of the ladder will be:

4/1.25 = 3.2m

(2) To perform the graduation of the x´yt´ axes, that is, the distance between the different spatial and temporal lines, we draw hyperbolas from the S axis to the S´ system:

To graduate the axes in S´ we draw hyperbolas from S to S´. It must be remembered that the equation of the hyperbola is X2-Y2=C2 which coincides exactly with the relativistic interval of Minkowsky space-time. If we look at the diagram the distance from the origin to point 1 will always be smaller than from the origin to 1´ therefore, the distance of the lines in S´ will be greater than in S and therefore the objects in S' will always have a smaller distance as dictated by the postulate of relativistic spatial contraction.

Sources:

The Theory of Relativity , TikZ.net