LOS FENÓMENOS MÁS EXÓTICOS DE LOS CAMPOS CUÁNTICOS
- planck
- 25 oct 2020
- 6 Min. de lectura
Actualizado: 26 dic 2024
Además de los fenómenos más conocidos y estudiados, el modelo estándar de la física de partículas incluye algunos efectos bastante más "exóticos" y menos conocidos. Estos efectos, denominados efectos no perturbativos tienen propiedades sorprendentes y a menudo están basados en un aspecto de la naturaleza que solo recientemente está siendo profundamente estudiado: la topología. Aunque en muchos estudios iniciales sobre campos cuánticos los efectos topológicos no eran considerados se ha demostrado que en muchos sistemas sus efectos son de una importancia capital tanto en mecánica cuántica (QFT) como en relatividad general. Estos efectos nos descubren un aspecto oculto pero fundamental de la naturaleza y nos conducen a través de los fenómenos físicos más exóticos y sorprendentes. En este artículo descubriremos algunos de estos increíbles fenómenos.
Geometrías no triviales
Imaginar que llegamos a un pequeño planeta de unos cientos de kilómetros de perímetro y queremos saber (sin explorarlo directamente) si tiene forma esférica o forma de "donuts". Imaginar que tenemos un dispositivo capaz de desplegar rápidamente en todas direcciones una cuerda capaz de abarcar toda la superficie del planeta. Entonces podemos activar nuestro dispositivo desde cualquier posición y volver a replegar la cuerda para recogerla. Si es posible replegar y guardar la cuerda en el dispositivo entonces estamos en una esfera, si la cuerda se queda atascada y no podemos replegarla entonces estamos en un planeta con forma toroidal (un donuts). Los espacios de la primera clase se denominan espacios simplemente conexos o de topología trivial, los de la segunda clase se denominan espacios de topología no trivial. Para transformar un espacio trivial en uno no trivial bastaría con quitar un único punto cualquiera: ahora ya no es posible contraer la cuerda ya que quedaría atascada en la posición que ocupaba ese punto. Esto es lo que trataremos de hacer en el próximo apartado.
Cuerdas de Dirac
A continuación, quitaremos un punto (mejor dicho una recta) de nuestro espacio (1)
Quizás te preguntes: ¿Como puede tener sentido algo así?
Consideremos un espacio libre de cualquier interacción física, este espacio es completamente simétrico: no existe ninguna coordenada ni ninguna dirección privilegiada. A continuación introducimos en nuestro espacio un solenoide muy largo (idealmente infinito) por el que pasa una corriente eléctrica. El solenoide se extiende a lo largo de la parte negativa del eje z:

Sea S la sección del solenoide, y "landa" la corriente por unidad de longitud. El campo magnético del solenoide puede considerarse como la suma de un gran número de pequeños dipolos magnéticos dm. El dipolo magnético entre una longitud z y otra z+dz será:

El dipolo magnético en el punto z=0 crea un potencial:

Por tanto el potencial total será:

El potencial es singular (infinito) justo para dos ángulos: 0 y PI. Estos dos ángulos describen por tanto una recta donde el potencial no está definido. Esta recta se denomina cuerda de Dirac y desde el punto de vista teórico es un objeto singular.
Desde el punto de vista del potencial podemos hacer cualquier cálculo en cualquier punto que este fuera de la recta. Es como si fuera necesario quitar la recta para que el potencial tenga sentido. Si esta recta es (idealmente) infinita nuestro espacio inicial queda "partido" o "no conectado" de forma que nuestro espacio trivial se ha convertido en un espacio con topología no trivial o un espacio con carga topológica.
Cargas topológicas
En el punto z=0 de nuestro eje z del apartado anterior tenemos una carga magnética de (Lambda*S/c), esta es la carga atribuida a un monopolo magnético (ver este artículo). Por esto los monopolos magnéticos, cuya existencia es predicha por nuestras teorías fundamentales están relacionados con cargas topológicas.
A continuación haremos algo un poco inusual: tomaremos nuestra carga magnética (nuestro monopolo magnético) y lo trasladaremos siguiendo un trayecto cerrado. Supongamos que tenemos un aparato que mide el trabajo realizado al desplazar la carga magnética. En ausencia de campos exteriores el medidor no cambia su lectura. A continuación, de forma similar al apartado anterior, vamos a transformar la "configuración topológica" de nuestro espacio. Para ello, introducimos un circuito eléctrico cerrado C2 que crea un campo electromagnético:

A continuación, pasamos cerca del circuito C2 pero el medidor sigue sin verse afectado. ¿Que sucede? Finalmente atravesamos la superficie C2 y el medidor aumenta una posición (que representa una cantidad fija de trabajo realizado). Da igual el camino que tomemos, lo largo que viajemos o lo cerca que estemos de C2 ¡ el medidor solo contará las veces que atravesamos la superficie C2 y siempre aumentará su valor en un número fijo!
La cantidad de veces que el monopolo (junto con su cuerda de Dirac) cruza la superficie S se denomina "winding number". Este número es un invariante topológico y como veremos, juega un papel muy importante en el modelo estándar.
Los infinitos vacíos del modelo estándar
Cuando la energía de nuestro Universo descendió por debajo de 246GeV se produjo una ruptura espontanea de simetría mediada por el campo de Higgs. En ese momento el potencial del campo cayó desde la cima hasta un punto cualquiera del círculo de mínima energía:
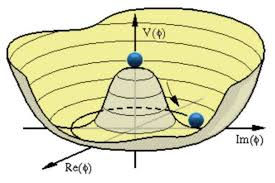
Este punto "elegido" al azar no es único, de hecho la simetría gauge implica que puedo escoger cualquier otro punto del círculo ya que son físicamente equivalentes. Esto significa que no existe un solo vacío en la teoría sino que existen infinitos vacíos posibles. Esto puede representarse de la siguiente forma:

Sin embargo, al incluir en nuestra teoría los posibles efectos topológicos aparece una sutileza, un fenómeno "exótico": los distintos vacíos pueden tener diferente "winding number" es decir, diferente carga topológica. Esto es debido a que las características del vacío vienen dadas por la fase del campo de Higgs. Esta fase, al ser compleja puede ser cualquier múltiplo de 2PI, es decir, la fase compleja puede haber dado cualquier numero de veces una vuelta completa y por tanto puede tener cualquier "winding number" en diferentes puntos del estado de vacío. Por esto, nos encontramos con que tenemos un conjunto infinito de estados de vacío con diferente carga topológica.
Instantones
En este apartado llegamos a las entidades más "exóticas" del SM. Como sabemos por los principios de la mecánica cuántica, una partícula encerrada en un potencial tiene una probabilidad no nula de escapar a través del efecto túnel. En el caso de los infinitos vacíos del SM existe una probabilidad de que el vacío "salte" de un valor a otro por efecto túnel. Esta probabilidad viene dada por unas entidades denominadas instantones:

La probabilidad de que una partícula "salte" por efecto túnel desde un mínimo de potencial a otro viene dada por un instanton. La probabilidad del "salto" inverso viene dada por un anti-instanton.
Los instantones son soluciones a las ecuaciones del Lagrangiano y se denominan así porque la transición se produce en un breve instante de tiempo. Los instantones representan una especie de túnel cuántico entre dos estados clásicamente desconectados:

Estas entidades tienen otra característica "exótica": el instante en el que se produce el "salto", su probabilidad y sus propiedades topológicas se calculan en tiempo complejo, es decir, en un espacio-tiempo Euclideo. Este espacio-tiempo con tiempo complejo parece jugar un papel fundamental para describir el efecto túnel cuántico, de hecho, existen modelos teóricos para describir el surgimiento de nuestro Universo por efecto túnel a través de una "burbuja de nada", es decir, una burbuja en un espacio-tiempo Euclideo.
Instantones y confinamiento
Uno de los problemas sin resolver más importantes del SM es explicar el fenómeno del confinamiento, es decir, explicar el mecanismo físico concreto que mantiene unidos a los quarks dentro del núcleo atómico. El núcleo atómico es un lugar complejo donde se encuentran "comprimidos" mares de quarks-antiquarks, gluones e instantones.
Aunque el fenómeno del confinamiento aún no es completamente conocido la idea general de como puede funcionar es bastante similar a lo que sucede en un superconductor: al atravesar un valor crítico de la energía se produce una ruptura espontánea de la simetría, los electrones (spin 1/2) forman estados ligados y se comportan como bosones (spin 1) que no respetan la estadística de Fermi y fluyen sin resistencia por una estrecha zona del conductor.
Dentro del núcleo atómico la imagen sería bastante similar:
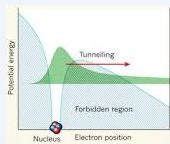
- Dos fermiones ligeros se encuentran separados por un potencial con forma de campana como el de la figura anterior. A través de la barrera de potencial empiezan a surgir pares de instantones-antiinstantones:

-Este intercambio de partículas produce una atracción que hace los quarks formen estados ligados. De forma análoga a los pares de Cooper en un superconductor estos pares ligados se comportan como bosones que forman un condensado de quarks.
- A continuación, este condensado de quarks hace que el estado de vacío se comporte como un superconductor: el campo gluónico es expulsado excepto en zona estrecha con forma de cilindro entre un quark y un antiquark. En esta zona el potencial es atractivo (debido a los gluones) y su valor aumenta linealmente con la separación entre los quarks, es decir, se comporta como una especie de cuerda que mantiene unidos a los quarks. ¡ Esto explica la fuerza que mantiene unida toda la materia del Universo !

En esta imagen del confinamiento el efecto túnel cuántico y los instantones juegan un papel fundamental. ¡ Los instantones pueden tener la explicación de porque existe toda la materia que vemos en el Universo!

Notas:
(1) Por "espacio" nos referimos al "espacio" matemático que contiene los campos gauge
Fuentes:







תגובות