¿ENTENDEMOS REALMENTE EL MUNDO QUE NOS RODEA?
- planck
- 24 sept 2012
- 10 Min. de lectura
Actualizado: 4 ene 2025
A menudo, cuando nos sucede algo imprevisto o algo que nos parece inusual solemos exclamar: "Así es la vida". Pero, ¿sabemos realmente que es la vida? Evidentemente eso que llamamos "vida", hablando desde el punto de vista social y humano (y por supuesto desde el punto de vista biológico pero en esto no entraremos) es algo muy complejo: es el resultado de millones de variables que varían en el tiempo e interactuan entre ellas de forma muy compleja creando un escenario dinámico y complejísimo imposible de predecir. A la naturaleza impredecible e incluso irracional a veces del cerebro humano hay que añadir la interacción de nuestro cerebro con cientos o miles de personas y con un conjunto de reglas o normas impuestas por el sistema social en el que estamos (sociales, profesionales, etc) y otras normas de carácter más innato (éticas, morales, etc).
Este complejísimo esquema tiene como consecuencia algo muy importante: un porcentaje altísimo de las cosas que nos suceden en la vida son fruto del azar (1). El problema es que nuestro cerebro, debido a la evolución y a su funcionamiento interno, busca siempre una causa a cualquier hecho que encontremos y le es muy difícil asimilar que un efecto no tenga causa, es decir, que sea fruto del azar. Esto es debido en parte a que el cerebro necesita saber que tiene cierto control sobre los efectos, no puede admitir la falta de control en nuestras vidas. Sin embargo, si analizamos nuestras vidas, enseguida nos daremos cuenta de que una gran parte de los acontecimientos más importantes que nos han sucedido han sido fortuitos, producto del azar: si el día que decidiste salir a tomar unas copas a la discoteca "Perfil" hubieras decidido (como casi sucede) quedarte en casa no hubieras conocido a tu mujer, si no hubiera habido una manifestación en tal calle no hubieras tenido que conducir por la calle donde tuviste el accidente, si tu jefe no hubiera enfermado no hubieras sido obligado a entrar en el "proyecto fatídico" aquel, si tu amigo empresario en lugar de tener un negocio de transportes tuviese una fábrica de pollos quizás tu tendrías un trabajo distinto, etc, etc.
Esto parece una mala noticia: apenas tenemos control sobre nuestras propias vidas, sin embargo, existe una buena noticia: aunque el azar, por su propia definición es impredecible, sí es cuantificable y aunque un suceso aislado es impredecible muchos sucesos examinados durante un tiempo a menudo si son predecibles por que contienen patrones cuantificables. Por supuesto, para realizar esto necesitamos a la ciencia, la estadística y los cálculos probabilísticos A continuación vamos a ver unos ejemplos de como todo esto afecta a nuestras vidas:
1º) La ilusoria relación entre éxito y cualidades personales
Muy a menudo, cuando vemos en la TV una entrevista a una persona de éxito (las modelos no cuentan) enseguida pensamos que esa persona tiene que tener unas cualidades personales extraordinarias. Nunca se nos ocurre pensar que gran parte de sus éxitos pueden ser fruto del puro azar. Por ejemplo, si calculamos que las probabilidades de éxito de una empresa en un determinado sector y en un determinado momento son del 5% y comprobamos que hay inscritas 100.000 empresas en el registro mercantil entonces, tenemos que esperar que solo por azar 5000 empresas tendrán un gran éxito mientras que el resto fracasará y consideraremos de forma incorrecta que esos 5000 directivos que dirigen esas 5000 empresas que han ganado millones son personas extraordinarias, con grandísimas dotes de dirección y gestión. Lo que realmente sucede es que muchos de los factores que deciden el éxito son aleatorios porque dependen de variables impredecibles: las ventas de una empresa recien creada y por tanto su éxito o fracaso dependen en gran medida de factores fortuitos: a un magnate le gustó el perro del anuncio de la empresa, a alguien le gustó la ubicación, un cliente importante tuvo una "corazonada", etc, etc). Por supuesto, esto no quiere decir que las cualidades personales y el esfuerzo no cuenten, de hecho son uno de los factores que aumenta las probabilidades de éxito, lo que sucede es que la relación entre el éxito y la destreza personal es mucho menos directa de lo que creemos y los factores aleatorios que nunca tenemos en cuenta son determinantes.
2º) Patrones aparentemente evidentes
Este es uno de los problemas más graves derivados del choque frontal entre nuestra intuición y el azar. El problema es que no sabemos identificar la huella del azar y atribuimos un significado a sucesos que en realidad son aleatorios, como resultado vemos patrones o regularidades cuando en realidad no hay nada y viceversa. Consideremos el siguiente ejemplo: supongamos que trabajamos en un departamento de I+D de una empresa de electrónica y que para estudiar el comportamiento de unos filtros de ruido electrónicos necesitamos una secuencia aleatoria muy grande de 0 y 1. Por tanto, encargamos a una empresa especializada un fichero con 101 millones de 0 y 1. El día que recibimos el fichero decidimos echarle un vistazo por curiosidad y entre toda esa enorme maraña de 0 y 1 aleatorios nos llama la atención una secuencia de 0 seguidos muy larga, con un programa, contamos la cantidad de 0 seguidos y descubrimos que hay ¡1 millón de 0 consecutivos! y lo que es aún peor, nuestro programa nos dice que hay 10 secuencias en total en el listado que contienen 1 millón de 0 seguidos. Evidentemente nuestra intuición nos dice que llamemos a la empresa especialista en crear números aleatorios y nos quejemos. Pero de nuevo nos equivocamos: en una secuencia de 101.000.007 ceros, la probabilidad de tener 10 subsecuencias de 1 millón de 0 seguidos es muy alta.
Este hecho tiene consecuencias asombrosas, imaginemos que una macroempresa tiene que afrontar tal cantidad de datos que se ve obligada a tomar una decisión de la forma todo (1) o nada (0) por segundo. Imaginemos que esta decisión se toma aleatoriamente y que analizamos los resultados de la empresa en un periodo de 3,25 años (una secuencia de 101 millones de 0 y 1 donde por ej. 0 representa el acierto y 1 el fallo), como hemos dicho, en esta secuencia encontraríamos que la empresa ha tomado 1 millón de decisiones acertadas seguidas durante 10 veces en ese periodo de tiempo. Lógicamente, los directivos de la empresa que estuviesen al frente de la misma en esos periodos serían vistos como "supergestores" mientras que los que encadenasen 1 millón (es de esperar que incluso bastante menos) de decisiones incorrectas serían despedidos fulminantemente. Sin embargo, en un periodo de 3,25 años ¡estas "rachas" se producirían simplemente por puro azar! La persona que estuviese al frente de una empresa que realiza por ejemplo operaciones bursátiles y que hubiese logrado por ejemplo una "racha" de 15 años consecutivos ganando por encima de las expectativas (cosa que ha pasado en la realidad) sería nombrada como una de las mejores gestoras de la historia. Los analistas calcularían las posibilidades de que esta racha suceda por casualidad obteniendo probabilidades bajísimas, pero, ¿calcularían correctamente estas probabilidades? Basándose en los precedentes, probablemente no. Estos analistas calculan las probabilidades escogiendo a un gestor en particular, en un mes en particular y haciéndose la siguiente pregunta en particular:
¿Cual es la probabilidad de que por pura suerte, la persona en concreto seleccionada batiera el mercado precisamente durante los 15 años siguientes? Sin embargo, esta no es la pregunta correcta, la pregunta correcta sería: ¿Cual es la probabilidad de que alguno de los MILES de administradores existentes durante TODO el periodo de la historia en el que han existido fondos de inversión batiera el mercado durante 15 años seguidos? Haciendo los cálculos con esta pregunta las posibilidades son muchísimo más altas, tanto, que lo extraño sería que no existiese ninguna empresa que lo consiguiese.
3º) Hechos aparentemente muy probables y viceversa
El fallo de nuestra intuición a la hora de calcular la probabilidad de que un acontecimiento suceda o no, se produce en muchos niveles diferentes. En este apartado veremos que incluso afecta a nuestra lógica. El problema es que la intuición confunde la probabilidad de que una serie de sucesos suceda si sucede algo con la probabilidad de que ese algo suceda si se produce esa serie de sucesos. Esto que parece un trabalenguas se entiende bien con unos ejemplos: Usted está convencido de que tiene una buena relación con su jefe, sin embargo, de repente, él parece tener una actitud más distante hacia usted: tarda más en contestar a tus preguntas y muestra una actitud más indiferente. Usted enseguida piensa que las probabilidades de que esto sucediese si te fueran a echar del trabajo son mucho más altas de lo que serían si todo fuese bien por lo que concluye que eso es lo que va a suceder en breve. Usted ha cometido un error muy común: ha confundido la probabilidad de que un conjunto de hechos (comportamiento ausente, tardanza en responder, etc) suceda si te van a echar del trabajo con la posibilidad de que te echen del trabajo si ese conjunto de hechos sucede. Si te fijas con atención la primera posibilidad es muy probable ya que si la junta directiva ha decidido recortar personal y tu nombre es uno de los elegidos es muy probable que tu jefe tenga una actitud distante hacia ti, sin embargo, la segunda, que es la que realmente nos interesa, es mucho menos probable ya que existen muchísimas razones potenciales que pueden motivar esa actitud a corto plazo: problemas con su mujer, exceso de trabajo, enfermedad de un familiar, etc, etc.
Otro ejemplo más general es el de las teorías de la conspiración: ante una serie de hechos, mucha gente piensa que la probabilidad de que sean producto de una conspiración oculta es mucho mayor de lo que realmente es, probablemente este hecho contribuye al florecimiento de "teorías" basadas en conspiraciones de todo tipo.
4º) Castigos y recompensas
Supongamos que eres el entrenador de un equipo que aspira a estar en las próximas olimpiadas de Londres en la modalidad de salto al potro. Tu experiencia te dice que cada vez que recriminas con fuerza a un deportista un salto malo entonces el siguiente salto casi siempre es mejor mientras que si elogias efusivamente un salto bueno el siguiente salto suele ser peor, por esto, tu experiencia e intuición te dice que es bueno castigar los saltos malos y que es malo recompensar los buenos. ¿Es esto correcto?. Como en casi todas las facetas de la vida, el azar juega aquí un papel muy importante: por puro azar habrá un porcentaje elevado de saltos que se podrán catalogar como saltos de calidad media o calidad esperada y un pequeño porcentaje de saltos que estarán por encima o por debajo de este nivel medio. Sucede que después de que el deportista haya ejecutado un salto muy bueno las posibilidades de que su siguiente salto este más cerca de la media (o sea que sea peor) son mucho más elevadas que las posibilidades de que vuelva a ejecutar un salto por encima de la media, y lo mismo sucede en el caso de un salto malo, su siguiente salto probablemente será mejor. Este fenómeno se denomina regresión a la media. Por tanto, está claro que el razonamiento del entrenador es erróneo, nuestra intuición y razonamiento han fallado totalmente, de hecho, experimentos psicológicos apuntan que lo mejor es lo contrario: recompensar los buenos saltos pero no castigar los saltos malos.
5º) Cuantificando errores aleatorios
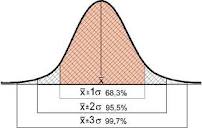
Una de las características más importantes que se deduce de las teorías del azar y que ha sido observada en todo tipo de situaciones es que si bien el error aleatorio intrínseco a cualquier medida o tarea que podamos realizar es impredecible, éste, cuando realizamos muchas medidas tiene un patrón claramente distinguible que tiene esta forma:
Esta es la llamada curva de la campana o distribución gaussiana. Esto quiere decir que si fabricamos por ejemplo 10.000 velas, la mayor parte de las ellas, que se corresponde con la media, tendrá las dimensiones buscadas, sin embargo, simplemente por azar debido a errores aleatorios, una parte de ellas se alejará de la media de forma que cuando el número fabricado es alto se cumple la curva de la campana. Esto ha sido observado en multitud de fenómenos en todos los campos imaginables: estaturas de personas, consumos de determinados productos, efectos de fármacos, etc etc. Este patrón en la aleatoriedad es tan fiable que se usa en la actualidad para detectar fraudes: existen gran cantidad de operaciones bursátiles regidas por la distribución normal, así es que se pueden detectar las desviaciones y vigilar las empresas cuyos datos no encajan en la curva de la campana.
Por ejemplo, hace varias décadas, analizando las estadísticas sobre las alturas de 100.000 jóvenes franceses llamados al servicio militar se detectó que la curva de la campana tenía una deformación correspondiente a unas 2200 personas justo por encima y por debajo de la altura mínima exigida para realizar el servicio militar: esos 2200 jóvenes probablemente manipularon un poco sus medidas para librarse del servicio militar. Para finalizar voy a poner un último ejemplo que ilustra lo importante que es manejar adecuadamente la información disponible y las técnicas estadísticas para llegar a resultados correctos. Como vimos en el punto 2, si tenemos una gran cantidad de datos o equivalentemente, si esperamos una gran cantidad de tiempo es muy probable que surjan por azar "patrones ficticios" es decir, patrones que son producto del puro azar.
Por ejemplo, si dividimos una gran ciudad en cuadrículas y analizamos la incidencia de cáncer en cada cuadrícula esperaremos que por puro azar algunos distritos estén por encima o por debajo de la media. Por ejemplo en una gran ciudad con 5000 cuadrículas esperaríamos encontrar por azar 2750 elevaciones significativas sobre la media. Sin embargo, en el caso del cáncer, la situación es todavía peor por que las cuadrículas no están fijadas de antemano sino que algún vecino alerta de que en su vecindario hay varios casos de cáncer y entonces fijamos el recinto a considerar (las cuadrículas) a posteriori, en la zona que se sabe que hay varios casos de cáncer. De esta forma las desviaciones de la media en algunas zonas parecen mucho más graves, con muchos casos por encima de la media. Este hecho produce que anualmente, los departamentos de salud de todo el mundo reciban decenas de miles de alertas con informes sobre grupos de cánceres residenciales, que derivan en cientos de exhaustivos análisis publicados (con el despilfarro económico y de recursos que eso conlleva) y "casualmente" ninguno identifica convincentemente una causa ambiental como causa de los cánceres. Seguro que ya han adivinado por que, y ya se habrán dado cuenta de lo importante que es identificar las huellas del azar en nuestras vidas.
PD: Este artículo pone una vez más de manifiesto la importancia de la ciencia no solo para obtener tecnología y mejorar nuestra calidad de vida sino también para entender el mundo que nos rodea y por tanto entendernos a nosotros mismos y como interaccionamos con el mundo exterior. Durante décadas, la mayor parte de la gente y de sus dirigentes han permanecido totalmente ignorantes en temas científicos lo que tiene una gran cantidad de consecuencias muy negativas: penosa gestión de los recursos, incorrecta valoración de las medidas políticas y económicas, escasa inversión en investigación...Quizás una extensa divulgación de estos temas empiece a cambiar la situación.
NOTAS: (1) El azar del que se trata en el artículo no es un azar puro en el sentido de que es totalmente aleatorio, sino que es un azar estocástico, es decir, que trata de procesos que aunque no dependen de procesos totalmente aleatorios, en la práctica, la cantidad de variables implicadas y su interacción es tan compleja y depende de forma tan sensible de las condiciones iniciales que no es posible de ninguna forma predecir su comportamiento y por tanto para todos los efectos prácticos son totalmente impredecibles y fortuitos.
Fuentes: El andar del borracho, 2008 Leonard Mlodinow

















Comentarios