STRING THEORY AND THE MICROSTATES OF BLACK HOLES

Currently, superstring theory (SST) is our best candidate for solving the biggest problem in fundamental physics: merging quantum mechanics and general relativity into a single theory. Many critics of string theory claim that it is too disconnected from the real physical world, that is, from our current low-energy Universe, and that it is therefore very difficult for the theory to make experimentally testable predictions. Although this is true in most cases (SST is a very high-energy theory), there are certain very specific cases in which this theory allows us to calculate the values of physical quantities of objects that exist in our current Universe. In this article, without resorting to complex mathematics, we will look at one such case, one that allows us to establish a spectacular link between string theory and our real world and that allows us to begin to glimpse the answer to what is probably the greatest enigma in physics: the fundamental nature of space-time.

Electrically charged black holes

Within general relativity, we can find solutions for spherical black holes (BLs) with no charge or rotation (Schwarzschild BLs), spherical black holes with electric charge but no rotation (Reissner-Nordstorm BLs), and spherical black holes with electric charge and rotation (Kerr-Newman BLs). In this article, we will look at the second case. These black holes have the following metric:

This metric has two horizons: an exterior one r+ and an interior one r-. This NA is described by only two charges: the mass M and the electric charge Q. There are three possible cases:

- M>Q: This case is physically the most common since real black holes tend to decrease their electrical charge by consuming matter from the outside.

- M=Q: This case constitutes what is known as an extreme black hole. In this case, the two horizons r+ and r- coincide, and Hawking radiation is zero.

- M

In this article we will focus on the second case, since, as we will see, it has some special properties.

The problem of black hole microstates

Black holes are, by far, the strangest and most fascinating objects in our known Universe. From the classical point of view, they are very simple objects; they can be described with only three physical quantities: mass, electric charge, and angular momentum. However, from the quantum (semiclassical) point of view, physicists have discovered that these objects have enormous entropy and therefore have an internal structure and must be composed of an enormous number of fundamental elements: microstates . Hawking and Bekenstein found that this entropy is S=A/4G, where A is the area of the NA measured in Planck units. This paradox clearly represents the problem of reconciling general relativity with quantum mechanics. What is the origin of these microstates? What are they composed of? Are these microstates the fundamental objects that constitute space-time? Although it may seem incredible, there is a specific case, a real black hole (1), in which we can count these microstates and "glimpse" their nature. This is what we will do next.

States in string theory

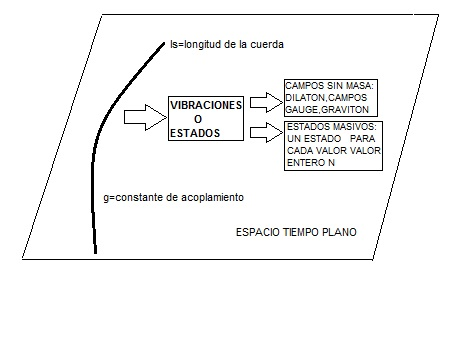
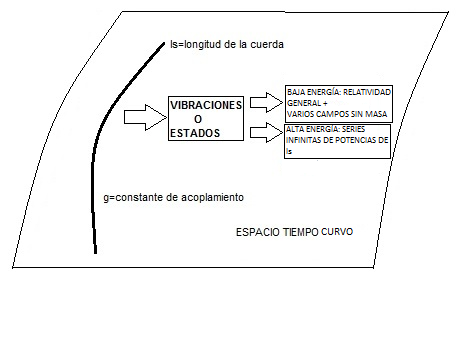
In string theory, we find that all particles are vibrations (states) of an extended one-dimensional object (a string). If we quantize a string in a flat spacetime, we obtain a finite set of massless states and an infinite set of massive states (one for each integer N) with M2=N/ls2 (where ls is the length of the string). If we quantize a string in a curved spacetime (typically a sphere or a torus), we obtain a spacetime with the Einstein metric coupled to a series of massless fields plus an infinite series of high-order terms in powers of ls. When the curvature is small compared to 1/ls2, then this infinite series of terms can be neglected. If we consider small curvatures and adjust certain parameters so that the extra scalar fields are zero, we can solve the low-energy equations and obtain a spacetime equivalent to that of general relativity. In fact, we obtain the following metric:

This is the metric of an extreme black hole! (2) The extreme NAs of Einstein's equations are solutions to the TSC equations!

From this result, we can deduce that an extreme AN is a very massive vibration state of a fundamental string. This happens because when the coupling exceeds a certain value, the generated gravitational field is so large that the string collapses, forming a black hole. All of this can be summarized in the following figures:

For the specific case of an extreme NA, there are certain states called BPS states that remain invariant for both weak and strong couplings. As we will see, these states will be key to studying the microstates of these NAs.

In addition to the above solution, there is another type of solution to the low-energy equations of the TSC: these solutions are known as solitons. Solitons are static and classical solutions to the equations. In field theories, solitons

The best known are monopoles and black holes themselves. Since the TSC "lives" in a 10-dimensional space-time, solitons can be monopoles or extended horizon objects (AN-type) of various dimensions, such as the so-called black branes or "black p-branes."

Types of charges in string theory

As we mentioned earlier, if we increase the coupling of a string (or a large number of strings) beyond a certain value, we will obtain a NA. If this NA is extreme, then, due to the invariance of BPS states with respect to increasing coupling, the initial string system and the final black hole will have the same number of states!

Our first task will be to identify some component or "object" of string theory that could be considered fundamental and that can be accounted for in some way. The main candidates that could meet this requirement are the charges of the SST. In the SST, there are two types of charges: NS-NS charges (for Neveu-Schwarz) and RR charges (for Ramond). At high coupling, we obtain black holes that can have NS-NS or RR charges, but with strong coupling, we don't know how to perform precise calculations. If we could identify which "objects" are equivalent to these charges at low coupling, perhaps we could move in the right direction. What types of objects are equivalent to NS-NS and RR charges at low coupling?

Similar to how a magnetic monopole carries a unit fundamental charge, if the object we want to identify were a soliton, it would carry a unit charge. The object that carries a unit NS-NS charge at low coupling is a vibration of a fundamental string. This is consistent with the previous identification between a BH and a massive state of a string. But what is the low-g equivalent of an RR charge? Initially, no known object seemed to have a unit RR charge; however, physicists subsequently found the fundamental component they were looking for: a "strange" multidimensional extended object whose vibrations were equivalent to those of open strings with their ends attached. These objects were called D-branes. These objects carry a unit R charge , and therefore, in our description, we can consider these objects to be the fundamental objects we are looking for! We are beginning to glimpse that these "strange" extended objects could be candidates to constitute the microstates of extremal black holes. The key question now is: Can we account for the states of these fundamental objects? If so, will their values match those predicted by the Bekenstein-Hawking entropy?

Building an extreme black hole with D-branes

Next, we want to construct an extreme NA with D-branes to try to count the number of states corresponding to that NA. For simplicity, we'll construct a 5-dimensional NA instead of a 4-dimensional one; however, it's also possible to construct a 4-dimensional extreme NA in a similar way.

If we put several D-branes together at a point in spacetime, they will form a bound state (similar to how electrons and protons form the bound state that constitutes an atom). If we take this bound state of N D-branes with charge QN at low coupling and increase g, we will obtain a BF. However, there is a problem: this BF has a singular horizon, that is, the metric diverges and becomes infinite at the horizon.

To solve this problem, we need to consider several types of charges instead of just one. Let us now consider an initial state with D-branes that have two types of charges that we will call Q1 and Q5 (this terminology will become clear later) that come together to form a single bound state BPS. If we now increase g, we find that the horizon of the BH is finite! (3) Now we have a real extremal BH!

The next question we ask is: Can we physically interpret these charge-bound states Q1-Q5?

To find the answer, we will consider the natural spacetime of the TSC: a flat 10-dimensional spacetime. Next, we compact 4 dimensions into a torus and 1 more dimension into a circle, thus having 5 macroscopic dimensions plus a 4-dimensional torus compacted into a circle (5 microscopic dimensions in total). In the 5 compacted dimensions, what fundamental elements could we identify with the charges Q1 and Q5? A rolled-up D-brane in one compact dimension carries one unit of R-charge (Q1), while a rolled-up D-brane in 5 compact dimensions would carry another unit of R-charge (Q5). These are the fundamental components that make up our black hole! Our 5-dimensional NA is composed of a bound state of 1-branes and 5-branes.

The key idea is this: there exist many different states with the same Q1Q5 charge, if we can count these states when g is small we can ensure (because BPS states hold as g increases) that the NA will have the same number of states. By counting how many states have the same Q1Q5 charge we get that their number increases with increasing number of D-branes, in the limit where the number of branes is very high (tends to infinity) we find that the number of states grows exactly as A/4G. This is the Bekenstein-Hawking entropy! This is the connection between string theory and real black holes!

Conclusions

To realize the importance of this result, we must remember that we started from a bound state of many elements carrying a fundamental unit of charge in a flat space-time (so we did not even start from a horizon to find that S=A/4G). and we have accounted for the number of different states with this load, regardless of how we compact the extra dimensions or the details of how the NA is formed as g increases the number of initial states must match the number of states in the final NA And this value exactly matches the Bekenstein-Hawking entropy! This is undoubtedly an impressive success for superstring theory.

String theory, as a candidate quantum theory of gravity, allows us to go beyond any semiclassical study and study new physical phenomena. For example, Hawking radiation itself can be described, in certain string models, as the decay of a non-BPS state produced by the collision of two open strings moving in opposite directions within a D-brane. This collision produces a closed string that leaves the brane located at the horizon, which constitutes Hawking radiation:

Another example would be the fact that in certain D-brane-based descriptions, the solutions to the equations continue into the horizon! In fact, the situation where a string falls into a BH is described by the process where a (closed) string transforms into an open string attached to a D-brane at the horizon:

Finally, there are indications that certain types of D-branes allow the geometry-topology of the space-time where they reside to be changed, giving rise to new space-time configurations ( see this article ).

The exciting adventure of finding the most fundamental components that make up the Universe we inhabit continues, and in this quest, the physical-mathematical framework of string theory is, without a doubt, the one most likely to provide the answer.

GRADES

(1) In the real universe, a charged black hole would tend to consume matter of the opposite charge and thus tend to decrease its charge. Despite this, its existence is theoretically possible under certain very specific conditions.

(2) This metric is actually that of a 5-dimensional extremal black hole. As explained later in the article, this metric has been chosen solely for simplicity, and it is perfectly possible to obtain the metric of a 4-dimensional extremal black hole from the low-energy equations of string theory.

(3) Actually we need 3 charges to construct an extremal black hole with a finite horizon (the other charge would be a string with some momentum in a compact direction), however, for practical purposes, we can consider that the fundamental charges are the charges Q1 and Q5.

Sources: The origin of black hole entropy in String Theory , Black holes in String Theory