SPACE-TIME BUBBLES AND TIME TRAVEL

One of the most shocking things that modern science has shown us is that the objective reality of the world around us is completely different from the "subjective reality" that our senses show us. Because of this, our common sense, so valuable in our daily lives, is hardly useful when we expose it to phenomena as counterintuitive as those described by Einstein's General Relativity: time dilation, curved space-time, black holes... These phenomena, as strange and counterintuitive as they may seem, have been demonstrated.

empirically and demonstrate that General Relativity describes our Universe with astonishing accuracy.

In this article, we'll delve into two of the strangest phenomena described by Einstein's theory: the possible existence of closed timelike curves and the possibility of time travel. We'll also take an absolutely incredible journey aboard a warp drive.

Welcome to an amazing world full of strange phenomena: our real Universe!

Metrics and different types of space-time intervals

Before starting, let's briefly review the basic concepts of metrics and the types of space-time intervals. Metrics measure the distances between two points in both flat and curved space-time. In flat spaces (Euclidean spaces), the distance between two points P(x1,x2,x3) and Q(x2,y2,z2) is obtained by applying the Pythagorean theorem in three dimensions:

|PQ|2=(x2-x1)2+(y2-y2)2+(z2-z1)2. If we take very small distances, that is, differential distances, and include time as a fourth dimension, we have the flat metric corresponding to special relativity (Minkowski space): ds2=-2dt2+dx2+dy2+dz2. This is the metric of our Universe in the absence of gravity. It is important to note that this metric defines a space-time interval in 4 dimensions; we are no longer measuring distances with a ruler, but spatial distances together with distances in the time dimension. The usual spatial distances are determined by the part of the metric given by dx2+dy2+dz2, for short we will call this interval D. The "temporal" length is given by -c2dt2 and is the distance that a ray of light travels in a given time, we will call this part T. In this way we can express the metric as: s2=D2-T2. Thus, there are three types of intervals:

- If D

- If D=T, the interval is "light-like." This is the distance traveled by a light ray.

- If D>T, the interval is "space-like." This is the least "usual" case: the spatial distance is greater than the temporal distance, so a ray of light does not have time to travel the spatial interval. There is no causal connection; this interval would correspond to superluminal travel (the observer would have to travel at a speed greater than c to cover the interval, which is not allowed).

Cylinders that drag space-time

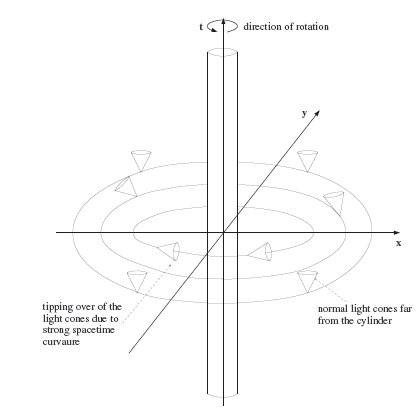
Next, we'll look at our first example of possible time travel. Imagine a (huge) cylindrical mass of stardust rotating in space-time. We can describe the metric of such an object as follows:

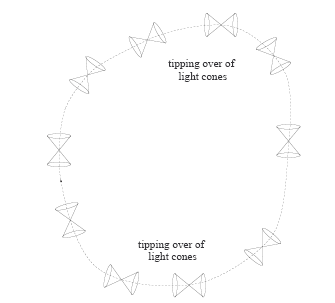
Where r is the radial distance, Ø is the angle of rotation of the cylinder, z is the distance along the axis of rotation, t is the time and the functions F(r), H(r), L(r) and M(r) are arbitrary functions that depend on r. In this metric any closed curve in the azimuthal direction Ø with t,r,z=cte has an invariant length s2=L(r)(2Π)2. In this closed path we have that if s2=L(r)(2Π)2=0 the trajectory is "light-like", if s2>0 it is "time-like" and if s2<0 it is "space-like". Thus, if we chose the function L(r) such that it takes negative values then we would have that the closed interval is "space-like", that is, going around the cylinder implies covering a distance at greater speed than light . We have made a superluminal trip!

Furthermore, this would imply something even stranger: this space-time curve is a closed time-like curve: any observer who makes the journey would return to the instant in time from which they started! How is this possible? The answer is that space-time is dragged by the rotating cylinder and if L(r) is negative the curvature of space-time is so great and the light cones are so curved that the time dimension "spins on itself" and returns to the starting point. Here we have a curve

closed time curve! At each turn within this closed curve we would have a time jump given by:

In "practice" this can be achieved with a very large (theoretically infinite) cylinder of radius R rotating with an angular velocity w>0.5c/R.

Of course, although theoretically possible, in practice this is almost impossible to achieve. Perhaps the only real physical system capable of possessing a closed timelike curve like the one we have seen is a rotating black hole (a Kerr black hole). Furthermore, it is also possible that various quantum effects (not considered in this article) make the existence of closed timelike curves impossible.

If the space-time metric produced by the rotating cylinder has a negative L(r) function, the curvature is so intense that any closed path in the direction of Ø will constitute a closed time-like curve. The light ray will have traveled into the past!

Traveling in a warp drive ship

General Relativity allows for solutions in which space-time curves, forming a kind of bubble. These solutions have inspired some physicists who have ventured to theoretically create something that seems entirely in the realm of science fiction: a kind of machine or ship capable of curving space-time around the bubble and thus traveling at speeds much greater than the speed of light. It should be noted that relativity prohibits travel at speeds greater than c in empty space, but nothing prohibits space itself.

space-time expand at speeds greater than c (as happened, for example, during cosmic inflation).

The idea is this: a ship (or whatever we want to transport) is placed inside the space-time bubble. The curvature we create must produce a compression of space-time at the front of the bubble and an equivalent expansion of space-time at the rear. In this way, the bubble and its interior will move forward at superluminal speeds, curving space. A science fiction fan's dream! An example of a metric that would produce a "warp-drive" effect would be the following:

Where the function f(x,y,z) must be 0 outside the bubble and 1 inside it. This metric is very simple: Outside the bubble (f=0) the metric is that of a flat spacetime (Minkowski metric): ds2=-dt2+dx2+dy2+dz2

Inside the bubble (f=1) the metric represents a sphere with center at (0,0,zo) moving along the z axis with velocity v(t) compressing the space-time in front of the bubble and expanding it at the rear in the same proportion.

If we choose a spherical function f we can study which are the geodesic trajectories to study the operation of our "Warp Drive":

As we wish the geodesic trajectories correspond to observers moving with the following 4-velocity:

That is, our traveler aboard the warp drive travels in the z direction with a speed v. The volume element is calculated by multiplying the variation of the metric (ds) in each of the directions of space-time. Since the only variation is in the z direction, we have that V=v(df/dz). In spherical coordinates, we have: V=v(z-z0)/r df(r)/dr. The factor 1/r causes that as r increases the volume decreases and vice versa: if r decreases the volume increases. The volume element decreases

in front of the bubble and increases behind it! This means that:

Space-time is contracting in front of the bubble and expanding behind it!

We can't finish without testing our warp drive. We sit aboard the ship, access the control panel, engage the warp drive, and observe the following on the space-time warp monitor:

The figure shows us that at the front of the bubble the volume increases while at the back it decreases.

Next we begin our journey: we will travel in a straight line along the z axis to the nearest star: Alpha Centauri, located 4.3 light years away. A light ray emitted at To=0 from Earth will reach Alpha Centauri in a time T1=D=4.3 years. Finally, we start our warp ship and head towards the nearest star with uniform acceleration "a" halfway and with uniform deceleration "-a" the other half. The distance traveled halfway with acceleration "a" will be: S1=1/2a(t/2)2 while in the second

route we will travel exactly the same distance S2=1/2a(t/2)2. Then S=S1+S2=a(t/2)2. Therefore, our ship will arrive at point Z=D in a time equal to: t=2√(D/a). The distance between the Earth and the star is: D2-T2=D2(1-4/aD).

Now comes the most shocking part: if our ship's acceleration is greater than 4/D, then D2 is greater than T2, so we've traveled a "space-like" distance and will therefore arrive at Alpha Centauri before the light beam! We've made a superluminal journey!

It is evident that implementing this in practice is, at present, completely out of our reach: we would need an immense amount of mass-energy to generate the desired curvature (metric) or significant amounts of

Exotic matter (as in wormholes), that is, matter with negative energy. Despite this, the fact that these solutions are theoretically admissible in General Relativity is truly surprising. Could we or some advanced civilization build something similar in the future?

Sources: Closed timelike curves and causality violation