MEASURING THE HOLOGRAPHIC DISPLAY OF A REAL BLACK HOLE

In 2019, the EHT (Event Horizon Telescopy) experiment showed the world the first "image" of a black hole. Physicists knew that the image data could hide important information about the black hole, about general relativity, or even shed some relevant light on quantum gravity. However, no one could have imagined that these data could hold one of the most important secrets about black holes and the nature of space-time. By carefully analyzing the EHT data, a group of physicists have made a truly fascinating proposal: the ring of photons surrounding the black hole may hide one of the most important secrets of quantum gravity; this ring of light may be part of the black hole's "holographic screen." If confirmed, this proposal would be an extraordinary advance: for the first time in the history of science, physicists could directly observe the effects of the so-called "holographic principle" and could gain access to the deepest secrets of space-time.

Holography and the microstates of the black hole

The Indian astrophysicist Subramanian Chandrasekhar once said that black holes are the simplest objects in the Universe because they can be completely described by just three quantities: mass, charge, and angular momentum. However, Stephen Hawking later showed that these objects, when quantum effects are considered, are not so simple: they radiate energy and therefore have a temperature and a set of associated microstates. Hawking calculated the number of microstates and found an enormous quantity: A/4, where A is the horizon area in Planck units. This showed that black holes (BH), although classically appearing to be simple objects, actually have a rich microstructure. But then, where is this enormous number of microstates found?

The first obvious candidate for hosting this structure is the event horizon or some interior region of the black hole close to the horizon. However, certain work based on extreme surfaces and holography seems to indicate that any object that falls into the NA is stripped of all its information before falling in. Furthermore, several theoretical calculations on particle interactions near the NA indicate that the calculations can only be correct if we also include regions outside the NA.

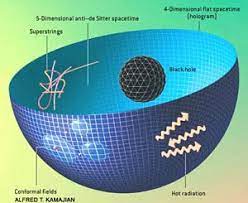
The so-called holographic principle is based on the AdS/CFT duality and states that all information about the geometry of the NA and its microstates (AdS geometry) is stored in a lower-dimensional conformal quantum field system (CFT). This is similar to how a hologram works: all the information in the three-dimensional hologram is stored on a two-dimensional surface. The crucial question physicists have been asking is: is there a three-dimensional region outside the black hole that meets the requirements to be the NA's "holographic screen" and can therefore store all the information in the four-dimensional NA? Although it may seem incredible, physicists have found a promising candidate: the photon ring surrounding the black hole.

The AdS/CFT correspondence implies that an AdS spacetime such as that of a four-dimensional black hole is equivalent to a conformal quantum system defined at the three-dimensional edge of AdS spacetime. The two systems are equivalent because they have the same set of fundamental symmetries and are therefore described by the same physics.

The black hole's photon ring

Photons of light passing near a black hole are deflected due to the strong curvature of space-time they produce. There is a critical radius above which photons can escape from the NA, and below which they will be absorbed forever. Near the critical radius, an extraordinary phenomenon occurs: photons will circle the black hole again and again until they finally escape or are absorbed. Within the sphere delimited by the critical radius, light would remain orbiting the NA forever. If an astronaut were to enter the area near the NA's photon ring, they would see a "movie" of all the events that have occurred around the NA; that is, they would see the entire history of the Universe as seen from the black hole (in fact, they would see infinite copies of every object in the Universe).

The region near the photon sphere is a very special one: it is the only region with a zero metric outside the black hole. This means that it acts as a "trapped surface" where light and gravitational waves are trapped (in fact, this region has characteristics similar to those of the event horizon). Because of this, this region behaves like the black hole's "resonance zone": high-frequency vibrations coming from the NA (which "vibrates" when "disturbed" by the matter falling into it until it returns to its equilibrium state) will be trapped in this zone. This is similar to the resonances emitted when we disturb (strike) a bell: the bell vibrates and emits waves whose frequencies are multiples of a specific value (the resonant frequency), which depends only on the geometry of the bell. By analyzing these frequencies, it is possible to calculate the geometry of the bell.

Similarly, much of the information about the geometry of the NA can be gleaned simply by observing the photon ring . These extraordinary properties are certainly reminiscent of the dual CFT of an AdS black hole. Have we finally found the black hole's holographic screen? However, one crucial ingredient is still missing: conformal symmetry. Would it be possible to find this symmetry in some feature of the photon ring?

The conformal symmetry of the photon ring

Conformal invariance is a powerful symmetry that plays a very important role in many fields of fundamental physics. In the AdS/CFT duality, the acronym "CFT" stands for "Conformal Field Theory" and refers to a field theory with conformal symmetry. Basically, this symmetry implies that a system remains invariant when observed at different scales. If we analyze the region near the photon sphere, we see that the layers closest to the critical radius have orbited the black hole more than the layers farther away. Studying the relationship between successive layers of the ring, we find that they are related by transformations of the SL(2,R) symmetry group (in phase space). This implies scale invariance between successive layers. It's hard not to draw a connection between conformal symmetry and holography when we encounter a structure like this linked to a black hole.

Experimentally measuring the black hole holographic screen

The AdS/CFT duality implies that both systems are physically equivalent, and therefore a "holographic dictionary" can be established between the magnitudes of AdS spacetime and those of the CFT conformal quantum system. As an example, some of the equivalences would be the following:

- The renormalization flux energy on the CFT side corresponds to the AdS spacetime radius of the black hole.

- The vibration modes of the AN corresponding to the so-called quasinormal modes correspond to the equilibrium fixed points (poles) of the CFT correlation functions.

- In certain models of string theory, the positions in AdS spacetime are given by the type of interactions between strings in the CFT.

The question we now ask ourselves is: Would it be possible to verify whether the photon sphere belongs to the AN's holographic screen by physically acting on it or on the AN? The answer, although theoretical, seems like science fiction: By throwing objects into the black hole, we could measure the response on the holographic screen and vice versa.

Recreation of the photon ring of a black hole (orange highlighted area)

Source: NASA's Goddard Space Flight Center/Jeremy Schnittman

The holographic principle implies that, in theory, the inverse relationship would be possible: acting on the holographic screen (CFT) we could modify the properties of the AN (AdS).

Upcoming black hole observation experiments are expected to be able to detect the photon ring and measure certain parameters of it. These parameters could give us fundamental clues about the physics involved in the holographic principle.

Conclusions

This fascinating proposal we have analyzed, if confirmed, could have enormous repercussions in various fields of fundamental physics. In addition to confirming the characteristics of holography, the AdS/CFT duality, and quantum gravity, it would have a major impact on resolving the information paradox of the NA: part of the information would be encoded holographically in the ring. This could be a clue pointing in the same direction as recent work based on the existence of "islands" in which information is stored in the NA and which may be located outside of it (see, for example, this article ). Perhaps the key question would be: What is the physical mechanism that allows information to be encoded holographically in the ring? What are the NA microstates? Are these microstates the fundamental components of spacetime?

Sources:

A black hole's orbiting ring of light could encrypt it's inner secrets , Holography of the Photon Ring