JOURNEY TO THE INFINITE EDGE OF THE UNIVERSE

Physicists and mathematicians have been discovering for some time now that our universe is much stranger and more fascinating than anyone could have imagined. Although it may seem impossible, modern mathematics and physics allow us, under certain circumstances, to treat infinity as if it were just another region of our universe and perform calculations on physical quantities that can be verified experimentally. We can reach and quantify infinity!

To make things even more interesting, physicists and mathematicians have recently discovered a fascinating physical-mathematical structure at infinity. This structure possesses new symmetries and new geometries, and more importantly, we can use it to perform calculations on experimentally verifiable physical quantities. In this article, we will explain the characteristics of this fascinating structure, which resides at the "infinity edge" of our Universe.

Celestial spheres and changes in coordinates

We will begin by looking at the concept of the celestial sphere for an observer at a given time. We define the celestial sphere as the set of all objects that are potentially observable (light has had time to reach it) by an observer at rest at a given time. This can be understood

Intuitively, it's like the sky an observer on Earth would see with an infinitely powerful telescope capable of capturing every photon from any part of the universe. This is graphically represented as follows:

The observer at point C will be able to see the sphere of light with radius r, since it takes a while for light to reach it. If we consider the sphere with r tending to infinity, we will see the entire sky visible from any angle we look at. This is the physical concept of the celestial sphere.

The vertical axis represents the expansion time of the light cone. The horizontal axes have been rotated 45º to coincide with the light cone by changing the coordinates u=ct+r. The cone starts at point A and expands in all directions at the speed of light. At time ct=B the light cone will have a radius r but an observer at point B will not be able to see it in its entirety since the light has not had time to reach their position. Said observer will have to wait until time ct=C to be able to see the entire sphere of light of radius r (this is represented by the red arrow in the drawing). For this reason, this coordinate system is called retarded coordinates or Bondi coordinates. If we consider the light cone

for r tending to infinity then we obtain the physical concept of a celestial sphere containing all points potentially visible from a point at a given instant of time.

The Riemann sphere

Consider a sphere at the center of the complex plane. Next, we draw a straight line connecting each point of the plane to the sphere's north pole. It's not difficult to see that for each point of the plane, there is one and only one straight line connecting that point to the north pole. Each line intersects the sphere at a different point, so we conclude that the sphere and the plane have exactly the same points!

All points on the (semi)sphere can be projected onto the complex plane. The points (circles) closest to the origin correspond to the lowest points on the sphere, while the points farthest from the plane correspond to the highest points. The north pole is the point located at infinity in the complex plane.

There is one exception: the North Pole. This point lies at infinity! Next, we'll see the relationship between the coordinate systems of the plane and the sphere.

The coordinates P' in the plane and those of the sphere P are related by the following change of coordinates: X'= RX/(R-X3) and Y'= RY/(R-X3). These coordinates can be grouped into a single complex coordinate: Z'=(X+iY)/(R-X3) which in polar coordinates would be written as: Z'= eiøtan(µ/2) where ø is the polar angle and µ is the azimuthal angle of the sphere. The function tan(µ) is an asymptotic function: as we move away

From the center we approach +-PI/2 but we only reach it at infinity!

Since the coordinate systems of the sphere and the plane are equivalent, we can use one or the other as appropriate. This implies something quite surprising: in the stereographic coordinate system (projection onto the plane), as we move outward, we get closer and closer to a kind of "edge" (the north pole of the sphere) but we never quite reach it: we can approach that "point" asymptotically, but we only reach it at INFINITY.

Consider the expanding light cone in the first figure in this article. If we cut the cone into horizontal slices, each slice represents a sphere of radius r. This can be represented in stereographic coordinates as a circle in the complex plane that increases in radius and approaches a value located on the "edge" asymptotically without ever reaching it:

In this representation, the inner circles represent spheres located further back in time, while the outer circles advance in time toward the edge. The edge represents asymptotic infinity (the north pole of the sphere). This would be the "infinity edge" of our Universe! The light cone that represents the past light cone (the celestial sphere that an observer sees at a given time) is called "Past Null Infinity" (I-). The light cone traveling into the future that a hypothetical observer would see

observer at the "infinity edge" is called "Future Null Infinity" (I+). This can be seen schematically in the so-called Penrose diagrams:

Future Null Infinity (I+) and Past Null Infinity (I-) are located 45º apart (following the light cones) in the future and in the past. Future Time Infinity (i+) and Past Time Infinity (i-) are infinitely separated in future and past time (t=infinity), and Spatial Infinity (io) is infinitely separated in space (r=infinity).

Symmetries and conserved charges

We know from Noether's theorem that every global symmetry implies a conserved physical quantity. Spatial symmetry implies the conservation of linear momentum, time symmetry implies the conservation of energy, and so on.

Let's look at our previous Riemmann sphere, which is equivalent to the complex plane. What are the symmetries of the sphere? That is, what transformations leave the sphere invariant? The obvious symmetries of the sphere are translations and rotations. These symmetries form a symmetry group called the Poincaré group, which plays a fundamental role in relativistic theories. The Poincaré group includes the Lorentz group, which is the symmetry group relating two inertial reference frames in special relativity. It can be shown mathematically that the Lorentz group is equivalent (isomorphic) to the group of symmetries of the sphere, which in turn (as we just saw) can be projected onto the complex plane. As a curious fact, it turns out that for two inertial observers moving at different speeds (for example one at rest and the other at 0.9c) and moving in the same direction, the relationship between both observers in the coordinates projected on the plane is: Z´=e-xZ. This means that while both are seeing the same

celestial sphere, the observer Z´ moving at 0.9c will see the celestial sphere compressed around the direction of motion. The moving observer will see the stars on the celestial sphere closer together than the observer at rest!

A ship traveling at speeds close to the speed of light will see the stars in the sky grouped around its direction of travel.

The image that appears in many science fiction films when the protagonist ship reaches speeds close to that of light is not correct: Physics tells us that the crew should see a contraction of the celestial sphere around the direction

of movement (the stars would be seen as points grouped around the center of the image).

But in addition to these symmetries, there is another, less obvious one: conformal symmetry. Basically, it's the symmetry that leaves the sphere invariant under changes in scale (more specifically, transformations that leave angles invariant). Mathematically, it can be shown that any transformation of the form Z(z)=az+b/cz+d is part of conformal symmetry. This is where the most interesting part comes in: physicists have recently discovered a new group of symmetries that reside in the "asymptotic" region of our Universe (what we previously called the "infinity edge"), and as we shall see, they may play a fundamental role in solving many of the greatest outstanding mysteries of physics.

Traveling to the "infinity edge" of the Universe

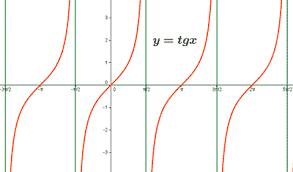
As we saw earlier, the polar coordinates (coordinates of the sphere) and the stereographic coordinates (coordinates of the projection of the sphere on the plane) are related by the function tg(x) which is an asymptotic function.

However, this change in coordinates is not unique; there are other changes that involve different asymptotic functions. For example, the electromagnetic field or the gravitational field decays as 1/r2 with distance r. This implies asymptotic behavior since the field will only be zero as r tends to infinity. The set of all possible spacetimes that asymptotically decay to 0 at infinity is called asymptotically flat spacetimes. The set of all these spacetimes (the set of their quantum properties) form a symmetry group (since they leave certain properties invariant) called the BMS group. This group operates at "null infinity" and is much larger than the Poincare group; in fact, it is an infinite group and therefore gives rise to an infinite number of conserved charges. The transformations that allow us to go from one element of the BMS group to another are called supertranslations.

The infinite charges would translate into an infinite number of new particles, called "soft gravitons" in the case of the gravitational field and "soft photons" in the case of the electromagnetic field. These particles would live in the "Null Infinity" and possess zero energy and momentum; however, (this is still being investigated) they could have polarization-angular momentum and therefore could carry information. These "soft particles" could hold the answer to one of the deepest questions in fundamental physics: the information paradox of black holes. These particles would also be found on the horizon of black holes (which is also a null surface like I+) and could constitute the physical medium where the information of the matter that falls into the black hole is stored. Physicist John Wheeler's famous phrase, "black holes don't have hair," could be false: perhaps they have an infinite amount of "hair." The existence of these hypothetical particles and their characteristics is currently one of the most active and important fields of research in theoretical physics.

Set of charges exchanging "Soft Photons"

It might seem that all this is just a mathematical structure without consequences for Physics, however, this is not true: encoded in the asymptotic geometry of Null Infinity is stored information about the momentum and energy of gravitational waves that have been radiated from the past to the Future Null Infinity (I+). By calculating this data stored in Null Infinity, we obtain the equations that describe gravitational waves in the exact nonlinear formulation of general relativity. These are the equations that have been used to model the recently discovered gravitational waves and therefore describe real physical quantities that can be verified experimentally.

Finally, it should be noted that the AdS/CFT duality relates a 4-dimensional spacetime with gravity to a 3-dimensional conformal quantum field theory. The latter resides at the infinite edge of the AdS Universe! and contains

all the information needed to describe the 4D Universe. Our Universe is not AdS but (approximately) dS, yet there is intense research underway to uncover the characteristics of a dS/CFT duality. Could it be that, following this holographic principle, all the information in our 4D Universe resides at the infinity edge? Modern Physics and Mathematics allow us to reach and quantify the "infinity edge" of our Universe, where perhaps lies the answer to many of the great mysteries of nature at a fundamental level!

Sources: From the Lorentz Group to the Celestial Sphere ; Geometry and Physics of Null Infinity , Soft Hair On Black Holes