GAUGE SYMMETRIES: BETWEEN THE REAL WORLD AND THE MATHEMATICAL WORLD

Although most people are not fully aware of it, there is a truly amazing world out there. At a fundamental level, the Universe is governed by physical laws so alien to our everyday common sense that they seem like science fiction. In this article, we will take a step-by-step look at one of the most important, profound, and transcendent concepts in modern Physics: the concept of gauge symmetry . Everything we know about particle physics, and therefore everything we know about the fundamental forces, is built on this fundamental concept. Furthermore, the existence of these symmetries allows us to make profound reflections on the nature of the Universe we inhabit and its fundamental laws: these laws seem to be halfway between the real physical world and the world of mathematics.

Global Gauge Symmetries

Symmetries can be divided into two large groups: "external" space-time symmetries (translations, rotations, etc.) and "internal" symmetries, which are internal degrees of freedom felt only by quantum fields (U(1), SU(2) symmetries, etc.). The former are simply called space-time symmetries, while the latter are called gauge symmetries.

In this article we will consider the latter since, although they are somewhat more abstract, they are as important (or more so) than the former.

Consider a fundamental particle described by a wave function.

The wave function is a complex function and, like any complex number, can be described by two values: a modulus and an angle. We know from the foundations of quantum mechanics that the probability of finding a particle at a specific point in space-time is given by the square of the modulus of the wave function. In fact, we know that only the modulus has physical meaning; the phase, therefore, is not physically measurable (*). This means that changing the phase has no physical effect. Therefore, if we multiply any wave function by the exponential function (which is equivalent to shifting the phase by an angle, since exp(iA)exp(iB)=exp(i(A+B)), the resulting wave function is physically equivalent to the previous one. The phase of a particle is a kind of "internal space" that particles feel and is therefore associated with a gauge symmetry (U(1) symmetry).

Every complex number can be represented as a vector formed by a module and an angle

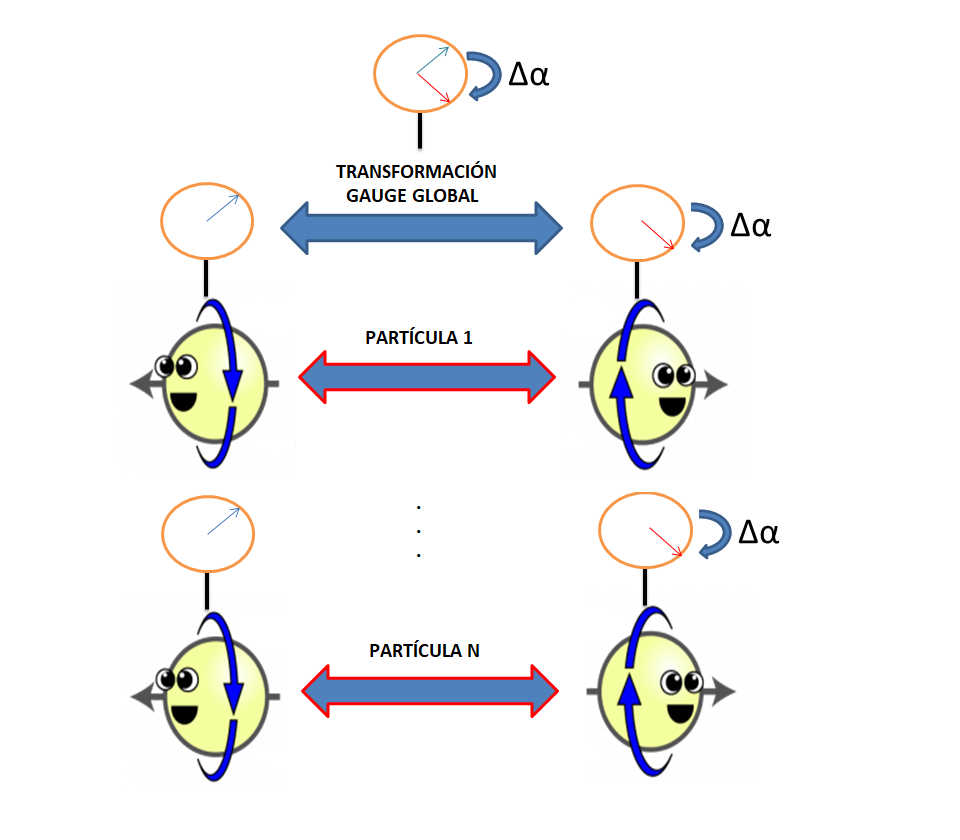
The example we have described is an example of global gauge symmetry since the transformation we have performed does not depend on space-time: by multiplying the wavefunction by exp(iB) we change the phase of all wavefunctions at all points in space-time by the same angle B.

By Noether's theorem we know that every global symmetry has a conserved charge, which implies the conservation of a physical magnitude, which is why symmetries are so important in Physics.

In a global U(1) gauge transformation, we change the same angle instantly to all particles, regardless of their location. This transformation has no physical effects on the particle.

Now we can ask ourselves: what would happen if we wanted to perform a local transformation instead of a global one, that is, a transformation in which the phase acquires a different angle depending on position and time? Can we do this without causing any physical effects?

Local Gauge Symmetries

As we know, relativity prohibits instantaneous interactions, so when studying fundamental particles and their interactions, we must transform global symmetries into local symmetries. This is where we encounter one of the most fundamental and profound concepts of modern physics: When trying to transform a global gauge symmetry into a local gauge symmetry , we break the symmetry . To preserve it, we have to add an extra term to the Lagrangian, and this extra term includes an interaction. This extra term represents a new quantum field: the gauge field , and it carries a conserved charge that represents a fundamental force, in this case the electromagnetic interaction . The key idea is that fundamental forces exist to preserve local gauge symmetries.

In a local U(1) gauge transformation, we modify each particle by a different angle depending on its space-time coordinates. This transformation would have physical effects on the particles if the electromagnetic force did not exist. The electromagnetic interaction exists to preserve the local U(1) symmetry.

Breaking and Restoring Gauge Symmetry

While "external" symmetries act by modifying an object in space-time, gauge symmetries typically act on a more abstract "object": the Lagrangian. Classically, the Lagrangian is defined as the difference between kinetic energy and potential energy. In quantum field theory, the Lagrangian is a functional defined in the Hilbert space where the wave function under consideration resides. In this case, we are talking about a "Lagrangian density" of all possible allowed states; therefore, at the quantum level, the Lagrangian operator is somewhat more abstract, although it is still clearly linked to the total energy of the system.

Often, the Lagrangian is not uniquely defined, but there are many different functions that describe the same Lagrangian. This is the meaning of gauge symmetry: transformations that leave the Lagrangian invariant . It's as if nature only cares about the total value of the Lagrangian, regardless of which functions produce that value.

The Lagrangian for a free particle of mass m is:

Where:

and the term "gamma" represents the famous Pauli matrices that satisfy:

Now we want to apply a local transformation that simply consists of changing the phase by an angle theta(x):

By applying this transformation to the Lagrangian and taking the derivative with respect to theta(x) we obtain:

As we can see, we have obtained our original Lagrangian , minus one extra term. This extra term did not appear when we performed the global transformation, since it is a derivative of the angle with respect to time, and if this angle is constant, the derivative is 0. Therefore, by performing this local gauge transformation, we obtain:

As we can see, we've broken the U(1) gauge symmetry. If we wanted to restore it, we'd have to try to counteract this new term. To do this, taking the derivative of the angle, we should obtain the following:

In this way, the new positive term would cancel the negative term we obtained previously, and symmetry would be restored. The new derivative we have defined is called the covariant derivative. Using it in our original Lagrangian, we obtain:

Thus, by applying the local gauge transformation with the new covariant derivative , symmetry is restored! The new A field we obtain is necessary to restore symmetry and is called the gauge field. The importance of this new field is enormous: it is responsible for all the technology that exists in our world, since it is the cause of electromagnetic interaction.

Gauge symmetries and fundamental forces

Let's look at the expression for the covariant derivative from the previous section. The first term is the usual derivative, the second term contains a coupling factor Q and the gauge field. This second term represents an interaction : in this case, the electromagnetic interaction.

In our low-energy Universe there are 4 fundamental forces: electromagnetism, the weak nuclear force, the strong nuclear force, and gravity.

The first three arise to locally restore the U(1), SU(2) and SU(3) gauge symmetries respectively. When our Universe had an energy above 246 GeV the U(1) and SU(2) symmetries formed a single SU(2)xU(1) symmetry called the electroweak symmetry such that the electromagnetic force and the weak force formed a single force. As the temperature decreased this symmetry broke down into the two forces we see today.

Imagine that we had access to a region of the Universe with a vacuum energy greater than 246 GeV (this could only happen in places where there are very high energies, such as at the center of mass of the LHC collisions or in certain specific areas near the horizon of magnetic black holes). In this region, electroweak symmetry would not be broken, and the quantum vacuum would be formed by a scalar field with a potential of the following form:

This potential has the famous Mexican hat shape:

The Lagrangian is the difference between kinetic energy and potential energy:

This Lagrangian is invariant not only under the U(1) symmetry that we have seen but also under the SU(2) symmetry since the Lagrangian does not change if we apply the following transformation (basically a rotation in the complex plane with respect to the vertical axis):

Where Ta are the generators of the SU(2) group which in this case are the Pauli matrices:

That is, the Lagrangian is invariant under SU(2)xU(1) symmetry. In case you haven't guessed, this field is the famous Higgs field.

To understand what happens in this high-energy region of the Universe, we can write the covariant derivative of the Lagrangian in the same way as we did in the previous section:

As in the case of U(1) symmetry that we saw previously, we have the usual derivative minus an interaction term. In this case we need to locally restore both U(1) and SU(2) symmetry, so the interaction term has 2 parts: the first corresponds to SU(2) symmetry and the second to U(1) symmetry. Now we need two gauge fields: the field A (with 3 components A1,A2,A3) and the field B. The term T2a represents the generators of the SU(2) group which are known as Pauli matrices and the factor Y represents the hypercharge which in this case is the unit matrix.

In this region of the Universe where we are, there is no electromagnetic force or weak force! There is only a scalar field with four gauge fields that behave identically to the photon we all know. Where we are, we can observe four different varieties of massless photons, and therefore, the electroweak force has an unlimited range !

By replacing the values of T2a in the previous expression we obtain:

Therefore the complete covariant derivative would be:

When our Universe cooled and the energy dropped below 246 GeV something extraordinary happened: the potential of our scalar field with its 4 gauge components "rolled down" from the unstable point at the top of "the hill" to a stable point of 0 potential at the bottom of the "Mexican hat".

This spontaneously breaks the SU(2)xU(1) symmetry, causing the field potential to stabilize at one of the points on the lower circle of the "hat." If we choose, for example, the following point (where h(x) is the radius of the circle):

We have that the covariant derivative becomes:

If we then define the following angle (the "blend" angle):

Where:

Then we can define the following fields:

This last expression shows something impressive: our four initial gauge fields (A1, A3, A3, B) have been transformed into four new fields that are linear combinations (mixtures) of the first ones. The fields W+, W- and Z are the carriers of the weak nuclear force and acquire mass due to the Higgs mechanism. while field A is the field carrying the electromagnetic force: the photon which remains massless.

The fields and forces we see in our Universe are a "mixture" of the fields and forces that already existed in the earliest moments of the Universe!

Conclusions

All this leads us to a deep reflection on how our Universe works at a fundamental level: The forces and fields that we see at low energies are the product of spontaneous symmetry breaking processes that happened at high energies and they exist to restore gauge symmetries at a local level. This means that the physics we see in our world is a consequence of a series of fundamental symmetries and symmetry breaking processes that happened in the early moments of the Universe. In fact, if these symmetries and symmetry breaking processes had been different, our world would be very different, for example, if the gauge field A had also acquired mass! The electromagnetic interaction would be short-range! Can anyone imagine such a world? (**)

On the other hand, it must be remembered that gauge symmetries are not symmetries linked to space-time, but rather symmetries associated with an internal space within quantum fields. Thus, these fundamental symmetries seem to exist halfway between the world of physics and mathematics.

It might seem that the fourth fundamental force, gravity, is excluded from this entire development based on gauge symmetries. However, this is not true; as we will see in the next article , gravity, and therefore space-time, can also be formulated as a gauge theory. This formulation leads us to a geometric view of the fundamental forces that will guide us toward a unifying theory of the four fundamental forces: the so-called "theory of everything."

Grades

(*) The phase of an individual particle is not measurable experimentally, although the phase difference of a group of particles is.

(**) Obviously, this situation would require a physical process of spontaneous symmetry breaking very different from what actually happened in our Universe: the Higgs mechanism of the standard model.

Sources:

Spontaneous Symmetry Breaking and the Higgs Mechanism. Andrew E. Blechman. December 13, 2000. Glashow-Weinberg-Salam Model: An Example of Electroweak Symmetry Breaking