SIMETRÍAS GAUGE: ENTRE EL MUNDO REAL Y EL MUNDO MATEMÁTICO
- planck
- 10 ago 2020
- 9 Min. de lectura
Actualizado: 26 dic 2024
Aunque la mayoría de la gente no sea muy consciente de ello ahí afuera existe un mundo realmente asombroso. A nivel fundamental el Universo se rige por unas leyes físicas tan ajenas a nuestro sentido común cotidiano que parecen ciencia ficción. En este artículo veremos paso a paso uno de los conceptos más importantes, profundos y trascendentes de la Física moderna: el concepto de simetría gauge. Sobre este concepto fundamental se construye todo lo que sabemos sobre física de partículas y por tanto todo lo que sabemos sobre las fuerzas fundamentales. Además la existencia de estas simetrías nos permite realizar profundas reflexiones sobre la naturaleza del Universo que habitamos y de sus leyes fundamentales: estas leyes parecen estar a mitad de camino entre el mundo físico real y el mundo de las matemáticas.
Simetrías Gauge Globales
Las simetrías pueden dividirse en dos grandes grupos: las simetrías "externas" espacio-temporales (traslaciones, rotaciones, etc) y las simetrías "internas" que son grados de libertad internos que solo sienten los campos cuánticos (simetrias U(1), SU(2), etc). Las primeras se denominan simplemente simetrías espacio-temporales mientras que las segundas se denominan simetrías gauge.
En este artículo consideraremos las segundas ya que aunque son algo más abstractas son tan importantes (o más) que las primeras.
Consideremos una partícula fundamental descrita por una función de onda.
La función de onda es una función compleja y como todo número complejo se puede describir por dos valores: un módulo y un ángulo. Sabemos por los fundamentos de la mecánica cuántica que la probabilidad de encontrar la partícula en un punto concreto del espacio-tiempo está dada por el cuadrado del módulo de la función de onda. De hecho sabemos que solamente el módulo tiene significado físico, la fase por tanto, no es medible físicamente (*). Esto quiere decir que cambiar la fase no tiene ningún efecto físico, por tanto, si multiplicamos cualquier función de onda por la función exponencial (lo que equivale a desplazar la fase un ángulo ya que exp(iA)exp(iB)=exp(i(A+B)) la función de onda resultante es físicamente equivalente a la anterior. La fase de la partícula es una especie de "espacio interno" que sienten las partículas y por tanto está asociada a una simetría gauge (simetría U(1)).

Todo número complejo se puede representar como un vector formado por un módulo y un ángulo
El ejemplo que hemos descrito es un ejemplo de simetría gauge global ya que la transformación que hemos realizado no depende del espacio-tiempo: al multiplicar la función de onda por exp(iB) cambiamos la fase de todas las funciones de onda en todos los puntos del espacio-tiempo el mismo ángulo B.
Por el teorema de Noether sabemos que toda simetría global tiene una carga conservada lo que implica la conservación de una magnitud física, por esto son tan importantes las simetrías en Física.
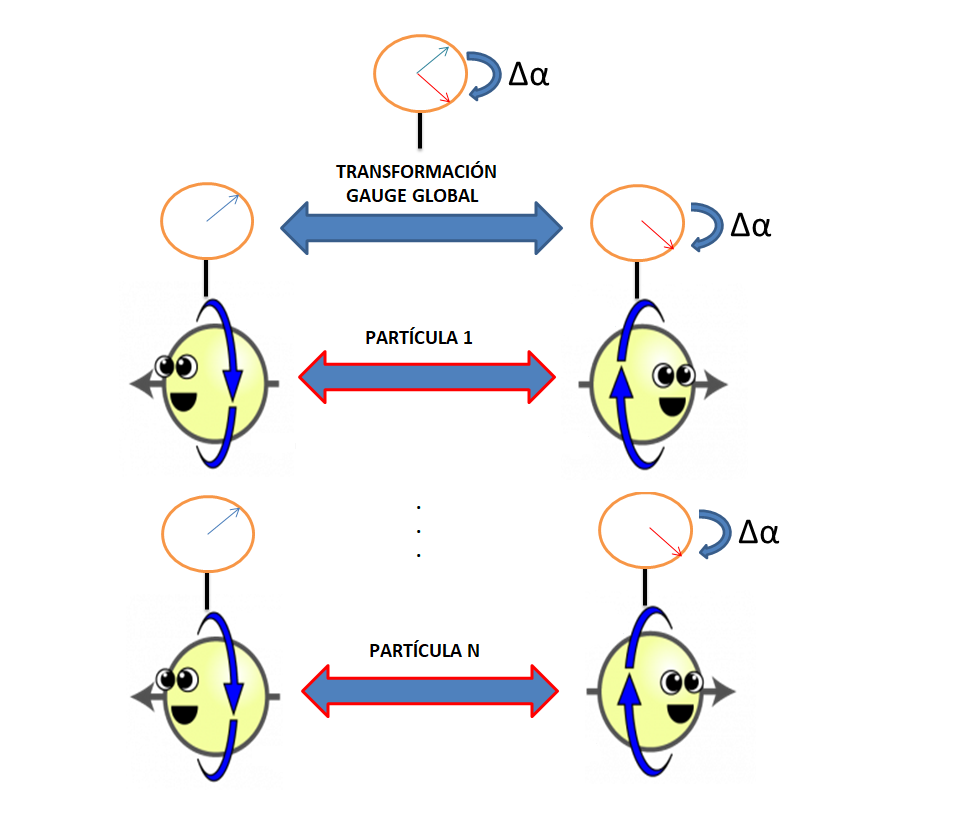
En una transformación gauge global U(1) cambiamos el mismo ángulo instantáneamente a todas las partículas sin importar su localización. Esta transformación no tiene efectos físicos sobre la partícula.
Ahora podemos preguntarnos: ¿que sucedería si queremos realizar una transformación local en lugar de global, es decir, una transformación en la que la fase adquiera un ángulo diferente en función de la posición y el tiempo? ¿Podemos hacerlo sin que haya efectos físicos?
Simetrías Gauge Locales
Como sabemos la relatividad prohíbe las interacciones instantáneas, por esto, a la hora de estudiar las partículas fundamentales y sus interacciones debemos transformar las simetrías globales en simetrías locales. Es ahora es cuando nos encontramos con uno de los conceptos más fundamentales y profundos de la física moderna: Al tratar de transformar una simetría gauge global en una simetría gauge local rompemos la simetría. Para conservarla tenemos que añadir un término extra en el Lagrangiano y este término extra incluye una interacción. Este término extra representa un nuevo campo cuántico: el campo gauge y porta una carga conservada que representa una fuerza fundamental, en este caso esta fuerza es la interacción electromagnética. La idea clave es que las fuerzas fundamentales existen para preservar localmente las simetrías gauge.

En una transformación gauge local U(1) modificamos un ángulo diferente a cada partícula dependiendo de sus coordenadas espacio-temporales. Esta transformación si tendría efectos físicos sobre las partículas si no existiera la fuerza electromagnética. La interacción electromagnética existe para preservar la simetría U(1) localmente.
Rompiendo y restaurando la Simetría Gauge
Mientras que las simetrías "externas" actúan modificando un objeto en el espacio- tiempo las simetrías gauge actúan típicamente sobre un "objeto" más abstracto: El Lagrangiano. Clásicamente el Lagrangiano se define como la diferencia entre la energía cinética y la energía potencial. En teoría cuántica de campos el Lagrangiano es un funcional definido en el espacio de Hilbert donde vive la función de onda que estamos considerando. En este caso hablamos de una "densidad Lagrangiana" de todos los estados posibles permitidos, por tanto, a nivel cuántico, el operador Lagrangiano es algo más abstracto aunque sigue claramente ligado a la energía total del sistema.
A menudo el Lagrangiano no está definido de forma única sino que hay muchas funciones diferentes que describen el mismo Lagrangiano. Este es el significado de la simetría gauge: transformaciones que dejan invariable el Lagrangiano. Es como si a la naturaleza solo le importara el valor total del Lagrangiano sin importar que funciones producen ese valor.
El Lagrangiano para una partícula libre de masa m es:

Donde:

y el término "gamma" representa las famosas matrices de Pauli que cumplen:

Ahora queremos aplicar una transformación local que consista simplemente en cambiar la fase un ángulo teta(x):

Al aplicar esta transformación en el Lagrangiano y hacer la derivada con respecto a teta(x) obtenemos:

Como vemos hemos obtenido nuestro Lagrangiano original Lo menos un término extra. Este término extra no aparecía cuando hicimos la tranformación global ya que es una derivada del ángulo con respecto del tiempo y si este ángulo es constante la derivada es 0. Por tanto, al hacer esta transformación gauge local obtenemos:

Como vemos, hemos roto la simetría gauge U(1), si quisiéramos restaurarla deberíamos tratar de contrarestar este nuevo término. Para lograrlo, al hacer la derivada del ángulo deberíamos de obtener lo siguiente:

De esta forma el nuevo término positivo cancelaría el término negativo que obtuvimos anteriormente y la simetría quedaría restaurada. La nueva derivada que hemos definido se denomina derivada covariante. Al utilizarla en nuestro Lagrangiano original obtenemos:

De esta forma al aplicar la transformación gauge local con la nueva derivada covariante ¡La simetría queda restaurada! El nuevo campo A que obtenemos es necesario para restaurar la simetría y se denomina campo gauge. La importancia de este nuevo campo es enorme: es el responsable de toda la tecnología que existe en nuestro mundo ya que es el causante de la interacción electromagnética.
Simetrías gauge y fuerzas fundamentales
Fijémonos en la expresión de la derivada covariante del apartado anterior. El primer término es la derivada usual, el segundo término contiene un factor de acoplamiento Q y el campo gauge. Este segundo término representa una interacción: en este caso la interacción electromagnética.
En nuestro Universo de baja energía existen 4 fuerzas fundamentales: el electromagnetismo, la fuerza nuclear débil, la fuerza nuclear fuerte y la gravedad.
Las tres primeras surgen para restaurar localmente las simetrías gauge U(1), SU(2) y SU(3) respectivamente. Cuando nuestro Universo tenía una energía por encima de los 246 GeV las simetrías U(1) y SU(2) formaban una única simetría SU(2)xU(1) denominada simetría electrodébil de forma que la fuerza electromagnética y la fuerza débil formaban una única fuerza. Al bajar la temperatura esta simetría se rompió en las dos fuerzas que vemos actualmente.
Imaginar que tuviésemos acceso a una región del Universo cuya energía del vacío es superior a 246 GeV (esto solo podría suceder en lugares donde existen altísimas energías como por ejemplo en el centro de masas de las colisiones del LHC o en algunas zonas concretas cerca del horizonte de agujeros negros magnéticos). En esta zona la simetría electrodébil no estaría rota y el vacío cuántico estaría formado por un campo escalar con un potencial de la siguiente forma:

Este potencial tiene la famosa forma de sombrero mejicano:

El Lagrangiano es la diferencia entre la energía cinética y la energía potencial:

Este Lagrangiano es invariante no solo bajo la simetría U(1) que hemos visto sino también bajo la simetría SU(2) ya que el Lagrangiano no cambia si aplicamos la siguiente transformación (básicamente una rotación en el plano complejo respecto al eje vertical):

Donde Ta son los generadores del grupo SU(2) que en este caso son las matrices de Pauli:

Es decir, el Lagrangiano es invariante bajo la simetría SU(2)xU(1). Por si no lo han adivinado este campo es el famoso campo de Higgs.
Para entender que sucede en esta zona del Universo de alta energía podemos escribir la derivada covariante del Lagrangiano de la misma forma que hicimos en el apartado anterior :

Como en el caso de la simetría U(1) que vimos anteriormente tenemos la derivada usual menos un término de interacción. En este caso necesitamos restaurar localmente tanto la simetría U(1) como la simetría SU(2) por esto el término de interacción posee 2 partes: la primera corresponde a la simetría SU(2) y la segunda corresponde a la simetría U(1). Ahora necesitamos dos campos gauge: el campo A (con 3 componentes A1,A2,A3) y el campo B. El término T2a representa los generadores del grupo SU(2) que son las conocidas como matrices de Pauli y el factor Y representa la hipercarga que en este caso es la matriz unidad.
¡ En esta zona del Universo en la que estamos no existe la fuerza electromagnética ni la fuerza débil ! Solo existe un campo escalar con 4 campos gauge que se comportan de forma idéntica al fotón que todos conocemos. ¡ Donde estamos podemos observar cuatro variedades diferentes de fotones sin masa y por tanto, la fuerza electrodébil tiene un alcance ilimitado !
Al sustituir los valores de T2a en la expresión anterior obtenemos:

Por tanto la derivada covariante completa sería:

Cuando nuestro Universo se enfrió y la energía bajó de 246 GeV sucedió algo extraordinario: el potencial de nuestro campo escalar con sus 4 componentes gauge "cayó rodando" desde el punto inestable en lo alto de "la colina" hasta un punto estable de potencial 0 en la zona baja del "sombrero mejicano".
Esto rompe de forma espontánea la simetría SU(2)xU(1) haciendo que el potencial del campo se estabilice en uno de los puntos del círculo inferior del "sombrero". Si elegimos por ejemplo el siguiente punto (donde h(x) es el radio del círculo):

Tenemos que la derivada covariante se transforma en:

Si a continuación definimos el siguiente ángulo (el ángulo de "mezcla"):

Donde:

Entonces podemos definir los siguientes campos:

Esta última expresión muestra algo impresionante: nuestros cuatro campos gauge iniciales (A1,A3,A3,B) se han transformado en cuatro nuevos campos que son combinaciones lineales (mezclas) de los primeros. Los campos W+ ,W- y Z son los portadores de la fuerza nuclear débil y adquieren masa debido al mecanismo de Higgs mientras que el campo A es el campo portador de la fuerza electromagnética: el fotón que permanece sin masa.
¡ Los campos y fuerzas que vemos en nuestro Universo son una "mezcla" de los campos y fuerzas que ya existían en los primeros instantes del Universo !
Conclusiones
Todo esto nos induce una profunda reflexión sobre como funciona nuestro Universo a nivel fundamental: Las fuerzas y campos que vemos a baja energía son el producto de procesos de ruptura espontánea de la simetría que sucedieron a altas energías y existen para restaurar las simetrías gauge a nivel local. Esto significa que la física que vemos en nuestro mundo es consecuencia de una serie de simetrías fundamentales y de procesos de ruptura de estas simetrías que sucedieron en los primeros instantes del Universo. De hecho, si estas simetrías y estos procesos de ruptura de simetría hubieran sido diferentes nuestro mundo sería muy distinto, por ejemplo, si el campo gauge A también hubiera adquirido masa ¡ La interacción electromagnética sería de corto alcance ! ¿Alguien puede imaginar un mundo asi? (**)
Por otro lado, hay que recordar que las simetrías gauge no son simetrías ligadas al espacio-tiempo sino que son simetrías asociadas a un espacio interno de los campos cuánticos. De esta forma estas simetrías fundamentales parecen tener una existencia a mitad de camino entre el mundo Físico y el mundo de las Matemáticas.
Pudiera parecer que la cuarta fuerza fundamental, la gravedad, queda excluida de todo este desarrollo basado en simetrías gauge. Sin embargo, esto no es cierto, como veremos en el siguiente artículo la gravedad y por tanto, el espacio-tiempo también puede formularse como una teoría gauge. Esta formulación nos conduce a una visión geométrica de las fuerzas fundamentales que nos guiará hacia una teoría unificadora de las cuatro fuerzas fundamentales: la llamada "teoría del todo".
Notas
(*) La fase de una partícula individual no es medible experimentalmente aunque si lo es la diferencia de fase de un grupo de partículas
(**) Evidentemente esta situación exigiría un proceso físico de ruptura espontánea de la simetría muy diferente del que sucedió realmente en nuestro Universo: el mecanismo de Higgs del modelo estándar
Fuentes:
Spontaneous Symmetry Breaking and the Higgs Mechanism. Andrew E. Blechman. December 13, 2000. Glashow-Weinberg-Salam Model: An Example of Electroweak Symmetry Breaking










Comentarios