BURBUJAS DE ESPACIO-TIEMPO Y VIAJES TEMPORALES
- planck
- 5 sept 2017
- 7 Min. de lectura
Actualizado: 1 ago 2025
Una de las cosas más impactantes que nos ha demostrado la ciencia moderna es que la realidad objetiva del mundo que nos rodea es completamente diferente de la "realidad subjetiva" que nos muestran nuestros sentidos. Por esto, nuestro sentido común, tan valioso en nuestra vida cotidiana apenas es de utilidad cuando lo exponemos a fenómenos tan contraintuitivos como los que describe la Relatividad General de Einstein: dilataciones temporales, espacio-tiempo curvo, agujeros negros... Estos fenómenos, por muy extraños y contraintuitivos que parezcan han sido demostrados
empíricamente y demuestran que la Relatividad General describe nuestro Universo con una precisión asombrosa.
En este artículo vamos a profundizar en dos de los fenómenos más extraños que describe la teoría de Einstein: la posible existencia de curvas cerradas de tiempo y la posibilidad de viajar en la dimensión temporal. Además realizaremos un viaje absolutamente increíble a bordo de una nave de curvatura o "Warp Drive".
¡Bienvenidos a un increíble mundo lleno de fenómenos extraños: nuestro Universo real !
La métrica y los distintos tipos de intervalos de espacio-tiempo
Antes de comenzar haremos un breve repaso de las nociones básicas del concepto de métrica y de los tipos de intervalos espacio-temporales. La métrica mide las distancias entre dos puntos tanto en el espacio-tiempo plano como en espacio-tiempo curvo. En espacios planos (espacios Euclidianos) la distancia entre 2 puntos P(x1,x2,x3) y Q(x2,y2,z2) se obtiene aplicando el teorema de Pitágoras en 3 dimensiones:
|PQ|2=(x2-x1)2+(y2-y2)2+(z2-z1)2. Si tomamos distancias muy pequeñas o sea diferenciales e incluimos el tiempo como cuarta dimensión tenemos la métrica plana correspondiente a la relatividad especial (espacio de Minkowski): ds2=-2dt2+dx2+dy2+dz2. Esta es la métrica de nuestro Universo en ausencia de gravedad. Hay que darse cuenta que esta métrica define un intervalo espacio-temporal en 4 dimensiones, ya no estamos midiendo distancias con una regla sino distancias espaciales junto con distancias en la dimensión temporal. Las distancias espaciales usuales las determinan la parte de la métrica dada por dx2+dy2+dz2, para abreviar a este intervalo lo denominaremos D. La longitud "temporal" viene dada por -c2dt2 y es la distancia que recorre un rayo de luz en un tiempo determinado, a esta parte la llamaremos T. De esta forma podemos expresar la métrica como: s2=D2-T2. De esta forma, existen tres tipos de intervalos:
- Si D<T el intervalo es "time-like". Este es un intervalo "usual": el tiempo "se mueve" más rápido que el espacio (como sucede en la mayoría de casos) y a la luz le da tiempo a recorrer el intervalo. Hay conexión causal.
- Si D=T el intervalo es "light-like". Este es el intervalo recorrido por un rayo de luz.
- Si D>T el intervalo es "space-like". Este es el caso menos "usual": la distancia espacial es mayor que la temporal por lo que un rayo de luz no tiene tiempo de recorrer el intervalo espacial. No hay conexión causal, este intervalo se correspondería con un viaje superlumínico (el observador debería viajar a velocidad mayor que c para cubrir el intervalo, cosa que no esta permitida)
Cilindros que arrastran el espacio-tiempo
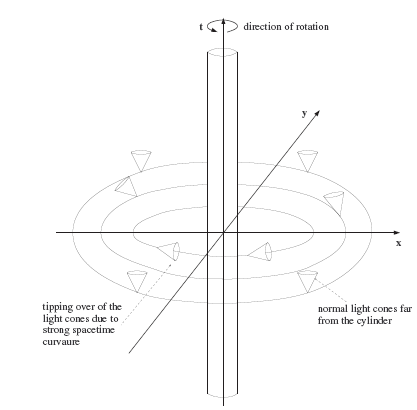
A continuación veremos nuestro primer ejemplo de posibles viajes temporales. Imaginar una (enorme) masa cilíndrica de polvo estelar que gira en el espacio-tiempo. Podemos describir la métrica de tal objeto de la siguiente forma:

Donde r es la distancia radial, Ø es el ángulo de giro del cilindro, z es la distancia sobre el eje de giro, t es el tiempo y las funciones F(r), H(r), L(r) y M(r) son funciones arbitrarias que dependen de r. En esta métrica cualquier curva cerrada en la dirección azimutal Ø con t,r,z=cte posee una longitud invariante s2=L(r)(2Π)2. En este trayecto cerrado tenemos que si s2=L(r)(2Π)2=0 la trayectoria es "light-like", si s2>0 es "time-like" y si s2<0 es "space-like". De esta forma, si escogiéramos la función L(r) de forma que esta tome valores negativos entonces tendríamos que el intervalo cerrado es "space-like", es decir, dar una vuelta alrededor del cilindro implica cubrir una distancia a mayor velocidad que la luz ¡Hemos realizado un viaje superlumínico!
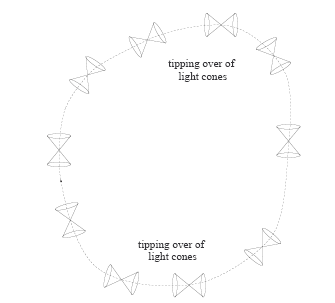
Además, esto implicaría algo aún más extraño: esta curva de espacio-tiempo es una curva temporal cerrada: cualquier observador que realice el trayecto ¡Volvería al instante de tiempo del que partió! ¿Como es esto posible? La respuesta es que el espacio-tiempo es arrastrado por el cilindro al girar y si L(r) es negativo la curvatura del espacio-tiempo es tan grande y los conos de luz están tan curvados que la dimensión temporal "gira sobre si misma" y vuelve al punto de partida. ¡ Aquí tenemos una curva
cerrada de tiempo ! En cada giro dentro de esta curva cerrada tendríamos un salto temporal dado por:

En la "práctica" esto puede lograrse con un cilindro de longitud muy grande (teóricamente infinito) de radio R que gire con una velocidad angular w>0.5c/R.
Por supuesto, aunque teóricamente es posible, en la práctica esto es casi imposible de conseguir. Quizás el único sistema físico real capaz de poseer una curva cerrada de tipo tiempo como la que hemos visto es un agujero negro rotatorio (agujero negro de Kerr). Además, es también posible que diversos efectos cuánticos (que no han sido tenidos en cuenta en este artículo) hagan imposible la existencia de curvas cerradas de tiempo.
Si la métrica del espacio-tiempo producida por el cilindro en rotación posee una función L(r) negativa la curvatura es tan intensa que cualquier camino cerrado en la dirección de Ø constituirá una curva cerrada de tipo tiempo ¡El rayo de luz habrá viajado al pasado!
Viajando en una nave de curvatura o "Warp Drive"
La Relatividad General admite soluciones en las que el espacio-tiempo se curva formando una especie de burbuja. Estas soluciones han inspirado a algunos Físicos que se han aventurado a realizar, de forma teórica, algo que parece pertenecer completamente al campo de la ciencia-ficción: una especie de máquina o nave capaz de curvar el espacio-tiempo alrededor de la burbuja y viajar así a velocidades mucho mayores que la velocidad de la luz. Hay que señalar que la relatividad prohibe viajar a velocidades mayor que c en el espacio vacío pero nada prohibe al propio
espacio- tiempo expandirse a velocidades mayores que c (como pasó por ejemplo durante la inflación cósmica).
La idea es la siguiente: dentro de la burbuja de espacio-tiempo se sitúa una nave (o lo que se quiera transportar). La curvatura que debemos crear debe producir una compresión del espacio-tiempo en la parte delantera de la burbuja y una expansión equivalente del espacio-tiempo en la parte trasera. De esta forma, la burbuja y su interior se moverán hacia adelante a velocidades superlumínicas curvando el espacio. ¡ El sueño de cualquier aficionado a la ciencia ficción ! Un ejemplo de una métrica que produciría un efecto "Warp-drive" sería la siguiente:

Donde la función f(x,y,z) debe ser 0 en el exterior de la burbuja y 1 en el interior de la misma. Esta métrica es muy sencilla: En el exterior de la burbuja (f=0) la métrica es la de un espacio tiempo plano (métrica de Minkowski): ds2=-dt2+dx2+dy2+dz2
En el interior de la burbuja (f=1) la métrica representa una esfera con centro en (0,0,zo) que se mueve a lo largo del eje z con velocidad v(t) comprimiendo el espacio-tiempo delante de la burbuja y expandiéndolo en la parte trasera en la misma proporción.
Si escogemos una función f esférica podemos estudiar cuales son las trayectorias geodésicas para estudiar el funcionamiento de nuestro "Warp Drive":

Tal como deseamos las trayectorias geodésicas se corresponden con observadores que se mueven con la 4-velocidad siguiente:

Es decir, nuestro viajero a bordo del motor de curvatura viaja en la dirección z con una velocidad v. El elemento de volumen se calcula multiplicando la variación de la métrica (ds) en cada una de las direcciones del espacio-tiempo. Como la única variación es en la dirección z tenemos que V=v(df/dz). En coordenadas esféricas tenemos: V= v(z-z0)/r df(r)/dr. El factor 1/r hace que a medida que aumenta r el volumen disminuya y al contrario: si r disminuye el volumen aumenta. ¡El elemento de volumen disminuye
delante de la burbuja y aumenta detrás de la misma! Esto quiere decir que:
¡ El espacio-tiempo se está contrayendo delante de la burbuja y expandiendo detrás de la misma !

No podemos terminar sin probar nuestra nave de curvatura "Warp Drive". Nos sentamos a bordo de la nave, accedemos al panel de control, encendemos el motor de curvatura y observamos en el "monitor de curvatura espacio-temporal" lo siguiente:

La figura nos indica que en la parte delantera de la burbuja el volumen aumenta mientras que en la parte trasera disminuye.
A continuación comenzamos nuestro viaje: viajaremos en linea recta a lo largo del eje z hasta la estrella más cercana: Alpha Centauri situada a 4,3 años luz de distancia. Un rayo de luz emitido en To=0 desde la Tierra alcanzará Alpha Centauri en un tiempo T1=D=4,3 años. Por fin, ponemos en funcionamiento nuestra nave de curvatura y nos dirigimos a la estrella más cercana con aceleración uniforme "a" la mitad del camino y con desaceleración uniforme "-a" la otra mitad del mismo. La distancia recorrida la mitad del trayecto con aceleración "a" será: S1=1/2a(t/2)2 mientras que en el segundo
trayecto recorreremos exactamente la misma distancia S2=1/2a(t/2)2. Entonces S=S1+S2=a(t/2)2. Por tanto, nuestra nave llegará al punto Z=D en un tiempo igual a: t=2√(D/a). La distancia entre la Tierra y la estrella es: D2-T2=D2(1-4/aD).
Ahora viene lo más impactante: si la aceleración de nuestra nave es mayor que 4/D entonces D2 es mayor que T2 por lo que hemos recorrido una distancia "space-like" y por tanto ¡Llegaremos a Alpha Centauri antes que el rayo de luz! ¡Hemos realizado un viaje superlumínico!
Es evidente que implementar esto en la práctica está, actualmente, totalmente fuera de nuestro alcance: necesitaríamos una inmensa cantidad de masa-energía que genere la curvatura (la métrica) deseada o bien cantidades importantes de
materia exótica (como en el caso de los agujeros de gusano), es decir, materia con energía negativa. A pesar de esto, el hecho de que teóricamente sean admisibles estas soluciones en la Relatividad General es realmente sorprendente. ¿Podremos nosotros o alguna civilización avanzada construir algo parecido en un futuro?











Comentarios