TODO FLUYE A LA VELOCIDAD DE LA LUZ
- planck
- 27 mar 2017
- 8 Min. de lectura
Actualizado: 27 dic 2024
Cierre los ojos y relájese cómodamente en su sofá o en su cama. Permanezca así durante 30 segundos y abra de nuevo los ojos. ¿No ha sentido nada especial? Probablemente no. Sin embargo, aunque usted no se haya dado cuenta ha realizado (sigue realizando) un viaje trepidante: ¡Usted ha viajado en el tiempo! ¡Ha viajado 30 segundos en la dimensión temporal sin salir de casa! Usted no se ha dado cuenta porque solo podemos ver las 3 dimensiones espaciales, sin embargo, el Universo que habitamos es un mundo de 4 dimensiones.
Cuando la Física moderna habla de la posible existencia de nuevas dimensiones del espacio-tiempo es muy usual sentir una sensación de rechazo y de incredulidad ya que nosotros solo podemos ver directamente 3 dimensiones. Sin embargo, nuestro Universo real en el que nos encontramos ya tiene una nueva dimensión "oculta": la dimensión temporal. Las 3 dimensiones espaciales parecen dominarlo todo y son omnipresentes, por el contrario, la 4ª dimensión es extraña: no parece una dimensión más y fluye de forma inexorable del presente al futuro. A pesar de ello, Einstein y Minkowski demostraron hace más de 100 años que nuestro espacio-tiempo es en realidad una estructura indivisible de 4 dimensiones. En este artículo visualizaremos la 4ª dimensión con conceptos sencillos y accesibles a cualquier persona con mínimos conocimientos Físicos, esto nos permitirá explicar de forma más natural fenómenos "extraños" como el spin y la naturaleza del tiempo. Además veremos como este "objeto" 4 dimensional junto con los 2 sencillos principios en los que se basó Einstein nos conducen a un Universo extraño y fascinante: el Universo real que habitamos.
El espacio-tiempo plano de Minkowski
Einstein se basó en 2 sencillos principios que son los siguientes:
1º) Las leyes de la Física deben ser las mismas en cualquier sistema de referencia que se mueva a velocidad constante.
2º) Todo observador, independientemente de su estado de movimiento medirá la misma velocidad de la luz: c.
El segundo principio ya implica algo sorprendente, puesto que un observador que se mueva a por ejemplo 3/4c tiene que medir siempre la velocidad c y v=x/t esto implica que el espacio y el tiempo no pueden ser absolutos, estos tienen que cambiar para observadores que se mueven a velocidades diferentes. Esto se entiende mejor con esta figura:

Consideremos dos sistemas de referencia S y S´. S está en reposo con respecto a S´ que se mueve a velocidad v con respecto a S. Consideremos que en el instante inicial ambos sistemas coinciden y en ese instante se emite un pulso de luz que se expande en todas direcciones formando una esfera. Lo que nos dice el 2º postulado es que ambos observadores deben medir la misma velocidad en la esfera de luz, es decir, el radio de la esfera debe ser el mismo para ambos observadores. La ecuación de la esfera en el sistema de referencia S es: X2+Y2+Z2=(ct)2 ya que el radio de la esfera es ct. Antes de seguir debemos notar algo muy interesante de esta expresión: todo observador de este Universo, esté en reposo, se mueva a 3/4c o a -1/2c está "embebido" en una esfera de radio ct. Esto nos da la primera pista sobre el origen del título de este artículo: todo observador puede considerarse como dentro de una esfera que viaja a c en 4 dimensiones. Como S y S' deben tener el mismo radio tenemos que X2+Y2+Z2-(ct)2=X'2+Y'2+Z'2-(ct)2'. Como S´se mueve solamente en el eje x tenemos que x'= x-vt mientras que y=y´y z=z. Sustituyendo y desarrollando los cuadrados obtenemos:

Ahora observamos que el nuevo término indeseable al desarrollar los cuadrados impide la igualdad. ¿Cual sería la transformación correcta para que la igualdad se cumpla? Está claro que hay que modificar x´y t´ de alguna forma: x´=a1x+a2t, y´=b1x+b2y. La clave es encontrar los coeficientes a1,a2,b1,b2. Visto desde S, S´es un punto que se mueve a velocidad v es decir x=vt, como en en instante inicial x=x´=0 entonces tenemos que x´=a1x+a2t=0, por tanto x=-a2/a1t=vt por tanto a2/a1=-v. Sustituyendo en nuestra
ecuación anterior obtenemos que x´=a1(x-vt). Desarrollando los cuadrados e igualando términos obtenemos:




Esto supone una de las revoluciones más grandes de la historia de la humanidad: el espacio y el tiempo no son absolutos, dependen del sistema de referencia. Sin embargo, como veremos, el "objeto" espacio-tiempo, considerado como un objeto 4-dimensional si es absoluto e inmutable.
Visualizando la entidad de 4 dimensiones
Consideremos que el eje x es la dimensión espacial y el eje y la dimensión temporal. Un intervalo de espacio-tiempo vendrá definido como:

Si ahora tenemos un segundo sistema de referencia S´que se mueve a velocidad relativa v´ respecto al anterior sistema tenemos:

El segundo sistema ha recorrido una distancia mayor que el anterior en el mismo tiempo t por tanto t´ aparecerá desplazado respecto a t. Para encontrar el segundo eje del segundo sistema de referencia S´consideramos la trayectoria de un rayo de luz que rebota en un espejo visto en el sistema de referencia S':

Para obtener la perspectiva de S´ dibujamos el eje ct' que obtuvimos anteriormente, prolongamos el eje hacia abajo y realizamos las intersecciones con este eje de los rayos de luz:

Lo que ha sucedido en S´es que los ejes han experimentado un giro, cuanto más se acerque a la velocidad a c mas se juntarán los ejes. Esto implica que sucesos que son simultáneos en un sistema de referencia no lo son en otro. Esto se ve claramente en esta figura:

En el sistema de referencia S los eventos E1 y E2 se producen en el mismo lugar (x=0) y en distintos instantes de tiempo. En el sistema de referencia S´los eventos E1 y E2 se producen en distintos lugares y distintos tiempos, además se puede apreciar que el intervalo espacial se acorta y el intervalo temporal se alarga en el sistema de referencia S´
Ahora es cuando podemos visualizar la cuarta dimensión en todo su esplendor: consideremos 2 naves espaciales que viajan a grandes velocidades (mayores que 1/2c) en dirección contraria y que se cruzan en una determinada región del espacio-tiempo,
llamaremos a esta región el intervalo A-B. ¿Que es lo que verán/medirán los pilotos de las naves espaciales al cruzarse? Verán lo siguiente:
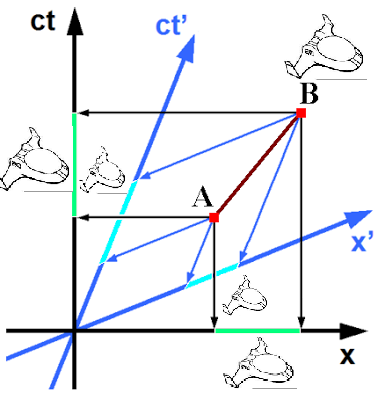
Las "sombras" del objeto 4D proyectadas en los ejes 3D: el segmento 4D A-B producirá una "sombra" sobre los ejes de mayor o menor longitud dependiendo del "ángulo de enfoque". Esa proyección es la que medimos en nuestros experimentos Físicos ya que solo podemos percibir 3 de las 4 dimensiones del espacio-tiempo.
El intervalo A-B es la longitud espacio-temporal "real" invariante, lo que mediría cualquier observador en reposo en la nave. El piloto en el sistema S medirá que la nave contraria tiene la longitud de la linea verde sobre el eje x y medirá el tiempo correspondiente a la linea verde sobre el eje ct. El piloto del sistema S´medirá la longitud de la linea azul sobre el eje x´y el tiempo de linea azul sobre el eje ct´. La clave aquí es la siguiente: ¡el intervalo real, el intervalo AB 4-dimensional es absoluto, no varía! El intervalo AB 4 dimensional puede puede tener mayor o menor componente espacial o temporal
pero su magnitud total en 4 dimensiones no varía. De alguna forma, lo que estamos viendo es la proyección desde distintos ángulos (en función del estado de movimiento) del mismo objeto 4-dimensional. ¡ Lo que vemos son las "sombras" tridimensionales de un objeto cuatridimensional !
Las partículas y las leyes fundamentales del Universo
Los 2 simples postulados anteriores tienen consecuencias de un alcance absolutamente impresionante, hasta el punto de que dictan como deben ser las leyes fundamentales de nuestro Universo. Analicemos el primer postulado: todas las leyes Físicas deben ser las mismas en cualquier sistema de referencia, sin embargo, ya vimos que tanto el espacio como el tiempo varían de un observador a otro así que ¿Cuales son las leyes Físicas que deben permanecer invariantes? Ya hemos visto una de ellas: el intervalo en 4 dimensiones.
Para saber cuales son los demás invariantes debemos utilizar la simetría. Como Noether demostró, toda simetría global posee una cantidad que se conserva: un invariante. La simetría espacial produce como consecuencia la conservación del momento lineal, la simetría temporal la conservación de la energía y la simetría de rotación la conservación del momento angular.
La simetría que deja invariante el intervalo 4 dimensional se denomina simetría de Poincaré. Esta incluye la simetría Lorentz y las traslaciones. La simetría de Poincaré implica la conservación de dos magnitudes: M2 y W2. M es la masa invariante (la masa en reposo) de la partícula y W es el momento total, es decir, la suma del momento lineal P y el momento angular J. La conservación de W explica uno de los fenómenos más misteriosos de la Física de partículas: el Spin. Imaginar una partícula de masa M en reposo. Todos los observadores deben observar las mismas leyes Físicas, es decir, el mismo valor de M2 y W2. W se compone de dos magnitudes P y J. Como P=0 entonces W=J. Todos los observadores deben observar el mismo valor de J. Pero ahora aparece un problema: consideremos un observador en un sistema de referencia que gira con velocidad angular constante alrededor de la partícula ¡Este observador verá a la partícula girando mientras que un observador en reposo junto a la partícula no observará ningún giro! La única forma de solucionar esto es que ¡la partícula en reposo gire también! ¡ Este giro intrínseco es el Spin !

Un observador en un sistema de referencia que gira alrededor de la partícula verá a esta girando mientras que un observador en reposo la verá parada. Esto esta prohibido por la relatividad y la simetría Lorentz-Poincaré.

La partícula debe girar para que todos los observadores perciban las mismas leyes de la Física
Pero hacer que la partícula gire crea otro problema: el sentido de giro establece una dirección privilegiada: imaginar que vamos en un coche y que nos movemos a la misma velocidad que un electrón que se mueve a lo largo del eje x. Si vamos "detrás" de el veremos que el electrón gira en un sentido determinado:

Sin embargo si adelantamos al electrón (cambiamos el sistema de referencia de izquierda a derecha, como en un espejo) ¡Veríamos que la partícula gira en sentido contrario¡ ¡ Pero esto no está permitido, todos los observadores deben medir el mismo valor del Spin ! ¿Como se puede solucionar esto? Para que las leyes fundamentales no cambien al cambiar el sistema de referencia es necesario "desdoblar" la partícula. El electrón posee dos componentes quirales que forman parte del spin: el componente de quiralidad "Left" y el componente de quiralidad "Right". Estos componentes constituyen los llamados "Spinors" de Dirac y son parte fundamental de la Ecuación Cuántica Relativista de Dirac. Cuando vamos "detrás" del electrón "veremos" la componente "Left" del mismo, al adelantar al electrón "veremos" la componente de quiralidad opuesta que tiene la misma dirección de Spin. De esta forma seguiremos viendo que el Spin (que es la magnitud invariante o conservada) no cambia, el sentido de giro es el mismo. ¡Por esto existen las partículas quirales! ¡La naturaleza "ha desdoblado" las partículas para cumplir con el primer postulado de la relatividad!

Todo fluye a la velocidad de la luz
Hemos visto que el espacio se puede "transformar" en tiempo y viceversa de forma que siempre se mantenga la misma magnitud de espacio-tiempo. Como sabemos que el momento lineal es el producto de la masa por la velocidad debemos esperar que también se mantenga invariante la magnitud de momento en 4 dimensiones.
Efectivamente el momento 4D es un invariante y se representa como P=(Po,Px,Py,Pz)=(Mc,Px,Py,Pz)=(E,Pxc,Pyc,Pzc). De la misma forma que con el espacio-tiempo, el "momento espacial" se puede transformar en "momento temporal" y viceversa pero siempre conservando la misma magnitud 4D. Si nos fijamos en el vector 4-momento,
el momento en la dimensión temporal Po se calcula multiplicando la masa en reposo por la velocidad de la luz. ¡Esto implica que puede considerarse a un cuerpo en reposo
como una masa que viaja a c en la dimensión temporal! Si aumentamos la velocidad (el momento) de dicho cuerpo, el vector 4-momento tendrá una componente temporal
menor y una componente espacial mayor. El fotón que viaja a c constituye el otro extremo: las componentes temporales son nulas y solo hay componente espacial.
Por esto, podemos considerar que en nuestro espacio-tiempo 4-D ¡ TODO FLUYE A LA VELOCIDAD DE LA LUZ !





Comentarios